【题目】在平面直角坐标系中,已知点A(-2,0),点B(0,4),点E在OB上,且∠OAE=∠OBA.
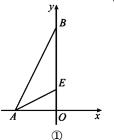
(1)如图①,求点E的坐标
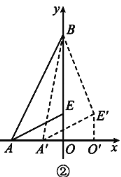
(2)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.
①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).
参考答案:
【答案】(1)(0,1)(2)①(1,1);②(![]() ,1).
,1).
【解析】
(1)根据相似三角形△OAE∽△OBA的对应边成比例得到![]() ,则易求OE=1,所以E(0,1);
,则易求OE=1,所以E(0,1);
(2)如图②,连接EE′.在Rt△A′BO中,勾股定理得到A′B2=(2-m)2+42=m2-4m+20,在Rt△BE′E中,利用勾股定理得到BE′2=E′E2+BE2=m2+9,则A′B2+BE′2=2m2-4m+29=2(m-1)2+27.所以由二次函数最值的求法知,当m=1即点E′的坐标是(1,1)时,A′B2+BE′2取得最小值.
(1)如图①,∵点A(-2,0),点B(0,4),
∴OA=2,OB=4.
∵∠OAE=∠0BA,∠EOA=∠AOB=90°,
∴△OAE∽△OBA,
∴![]() ,即
,即![]() ,
,
解得OE=1,
∴点E的坐标为(0,1);
(2)①如图②,连接EE′.
由题设知AA′=m(0<m<2),则A′O=2-m.
在Rt△A′BO中,由A′B2=A′O2+BO2,得A′B2=(2-m)2+42=m2-4m+20.
∵△A′E′O′是△AEO沿x轴向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=m.
又∵BE=OB-OE=3,
∴在Rt△BE′E中,BE′2=E′E2+BE2=m2+9,
∴A′B2+BE′2=2m2-4m+29=2(m-1)2+27.
当m=1时,A′B2+BE′2可以取得最小值,此时,点E′的坐标是(1,1).
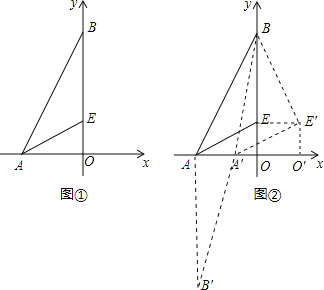
②如图②,过点A作AB′⊥x,并使AB′=BE=3.
易证△AB′A′≌△EBE′,
∴B′A′=BE′,
∴A′B+BE′=A′B+B′A′.
当点B、A′、B′在同一条直线上时,A′B+B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
∴![]() ,
,
∴![]() ,AO=2,
,AO=2,
∴AA′=![]() ×2=
×2=![]() ,
,
∴EE′=AA′=![]() ,
,
∴点E′的坐标是(![]() ,1).
,1).
-
科目: 来源: 题型:
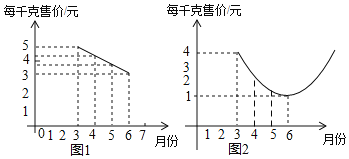
查看答案和解析>>【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )

A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3),B(-3,2),C(-1,1).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A'B'C'与△ABC是位似图形,请写出位似中心的坐标:______;
(4)顺次连接C,C1,C',C2,所得到的图形是轴对称图形吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 和y=
和y= 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=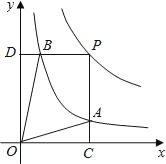 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=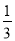 AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )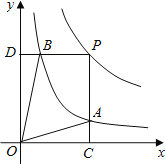
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=x+2的图象与函数y=
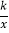 (k≠0)的图象交于A、B两点,连接BO并延长交函数y=
(k≠0)的图象交于A、B两点,连接BO并延长交函数y=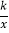 (k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
(k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.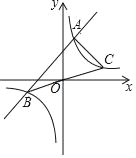
相关试题

