【题目】如图,在直角坐标系中,点A的坐标为(﹣2,0),OB=OA,且∠AOB=120°.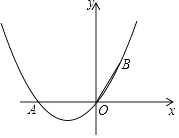
(1)求经过A,O,B三点的抛物线的解析式.
(2)在(1)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M,N使得A,O,M,N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB= ![]()
∴点B的坐标是(1, ![]() ).
).
设所求抛物线的解析式为y=ax2+bx+c,
由已知可得: 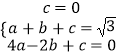 ,
,
解得: 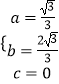
∴所求抛物线解析式为y= ![]() .
.
(2)
解:存在,
∵△BOC的周长=OB+BC+CO,
又∵OB=2
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称
∴连接AB与对称轴的交点即为点C,
且有OC=OA
此时△BOC的周长=OB+BC+CO=OB+BC+AC;
点C为直线AB与抛物线对称轴的交点
设直线AB的解析式为y=kx+b,
将点A(﹣2,0),B(1, ![]() )分别代入,得:
)分别代入,得:
![]() ,
,
解得: 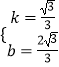 ,
,
∴直线AB的解析式为y= ![]() x+
x+ ![]()
当x=﹣1时,y= ![]() ,
,
∴所求点C的坐标为(﹣1, ![]() );
);
(3)
解:如图,
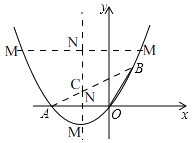
①当以OA为对角线时,
OA与MN互相垂直且平分
∴点M(﹣1,﹣ ![]() ),
),
②当以OA为边时
OA=MN且OA∥MN
即MN=2,MN∥x轴
设N(﹣1,t)
则M(﹣3,t)或(1,t)
将M点坐标代入y= ![]() .
.
∴t= ![]()
∴M(﹣3, ![]() )或(1,
)或(1, ![]() )
)
综上:点M的坐标为:M(﹣1,﹣ ![]() )或(﹣3,
)或(﹣3, ![]() )或(1,
)或(1, ![]() ).
).
【解析】(1)先确定出点B坐标,再用待定系数法即可;(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;(3)分OA为对角线和为边两种情况进行讨论计算.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?
-
科目: 来源: 题型:
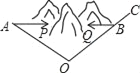
查看答案和解析>>【题目】(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售人员本月的销售量(单位:台)进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的中位数、众数分别是( )

A. 20台,14台 B. 19台,20台 C. 20台,20台 D. 25台,20台
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )

A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4 -
科目: 来源: 题型:
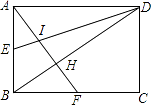
查看答案和解析>>【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
A.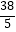
B.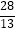
C.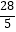
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
相关试题

