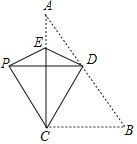
【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,若△PCD中有一个角等于50°,则∠A度数等于__.
参考答案:
【答案】40°或25°.
【解析】
由折叠的性质得出AD=PD=BD,∠CPD=∠B,∠PDC=∠BDC,∠PCD=∠DCB,由直角三角形斜边上的中线性质得出CD=![]() AB=AD=BD,由等腰三角形的性质得出∠ACD=∠A,∠DCB=∠B,然后分三种情况求解即可.
AB=AD=BD,由等腰三角形的性质得出∠ACD=∠A,∠DCB=∠B,然后分三种情况求解即可.
由折叠可得,AD=PD=BD,∠CPD=∠B,∠PDC=∠BDC,∠PCD=∠DCB,
∴D是AB的中点,
∴CD=![]() AB=AD=BD,
AB=AD=BD,
∴∠ACD=∠A,∠DCB=∠B,
当∠CPD=50°时,∠B=50°,
∴∠A=90°﹣∠B=40°;
当∠PCD=50°时,∠DCB=∠B=50°,
∴∠A=40°;
当∠PDC=∠BDC=50°时,
∵∠BDC=∠A+∠ACD,
∴∠A=![]() ∠BDC=25°;
∠BDC=25°;
故答案为:40°或25°.
-
科目: 来源: 题型:
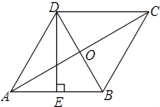
查看答案和解析>>【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A. 3 B. 3
 C. 2
C. 2 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A.1个B.2个C.3个D.3个以上
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A和对称中心在反比例函数y=
 (k≠0,x>0)上,若矩形ABCD的面积为8,则k的值为( )
(k≠0,x>0)上,若矩形ABCD的面积为8,则k的值为( )
A. 8 B. 3
 C. 2
C. 2 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】请利用直尺完成下列问题
(1)如图(1)示,利用网格画图:

①在BC上找一点P,使得P到AB和AC的距离相等;
②在射线AP上找一点Q,使QB=QC.
(2)如图(2)示,点A,B,C都在方格纸的格点上.请你再找一个格点D,使点A,B,C,D组成一个轴对称图形,请在图中标出满足条件的所有点D的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是直线y=﹣x上的动点,点B是x轴上的动点,若AB=2,则△AOB面积的最大值为( )

A. 2 B.
 +1 C.
+1 C.  -1 D. 2
-1 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
如图①,在△ABC的边AB上取一点P,连接CP,可以把△ABC分成两个三角形,如果这两个三角形都是等腰三角形,我们就称点P是△ABC的边AB上的和谐点.

解决问题:
(1)如图②,在△ABC中,∠ACB=90°,试找出边AB上的和谐点P,并说明理由:
(2)己知∠A=36°,△ABC的顶点B在射线l上(如图③),点P是边AB上的和谐点,请在图③及备用图中画出所有符合条件的点B,用同一标记标上相等的边,并写出相应的∠B的度数.
相关试题

