Question

【题目】（1）如图1，在△ABC中，∠ACB＝2∠B，∠C＝90°，AD为∠BAC的平分线交BC于D，求证：AB＝AC＋CD．（提示：在AB上截取AE＝AC，连接DE）

（2）如图2，当∠C≠90°时，其他条件不变，线段AB、AC、CD又有怎样的数量关系，直接写出结果，不需要证明．

（3）如图3，当∠ACB≠90°，∠ACB＝2∠B ，AD为△ABC的外角∠CAF的平分线，交BC的延长线于点D，则线段 AB、AC、CD又有怎样的数量关系？写出你的猜想，并加以证明．

Answer 1

【答案】（1）见解析；（2）AB＝AC＋CD；（3）AB＝CD﹣AC

【解析】试题分析：（1）在AB上截取AE=AC，连接DE，根据角平分线的定义得到∠1=∠2．推出△ACD≌△AED（SAS）．根据全等三角形的性质得到∠AED=∠C=90，CD=ED，根据已知条件得到∠B=45°．求得∠EDB=∠B=45°．得到DE=BE，等量代换得到CD=BE．即可得到结论；

（2）在AC取一点E使AB=AE，连接DE，易证△ABD≌△AED，所以∠B=∠AED，BD=DE，又因为∠B=2∠C，所以∠AED=2∠C，因为∠AED是△EDC的外角，所以∠EDC=∠C，所以ED=EC，BD=EC，进而可证明AB+BD=AE+EC=AC；

（3）在AB的延长线AF上取一点E，使得AE=AC，连接DE．证明△ACD≌△AED，根据全等三角形的性质得到DE=BE，BE=CD，即可得出结论．

试题解析：（1）证明：在AB上取一点E，使AE=AC

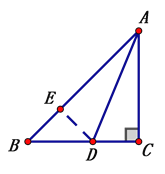
∵AD为∠BAC的平分线

∴∠BAD=∠CAD．

在△ACD和△AED中，

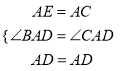
∴△ACD≌△AED（SAS）．

∴∠AED=∠C=90°，CD=ED，

又∵∠ACB=2∠B，∠C=90°，

∴∠B=45°． ∴∠EDB=∠B=45°．

∴DE=BE， ∴CD=BE．

∵AB=AE＋BE， ∴AB=AC＋CD．

（2）证明：在AB取一点E使AC=AE，

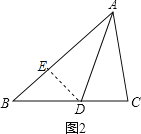
在△ACD和△AED中，

,

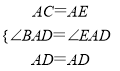∴△ACD≌△AED，

∴∠C=∠AED，CD=DE，

又∵∠C=2∠B，

∴∠AED=2∠B，

∵∠AED是△EDC的外角，

∴∠EDB=∠B，

∴ED=EB，

∴CD=EB，

∴AB=AC+CD；

（3）猜想：AB=CD﹣AC

证明：在BA的延长线上取一点E，使得AE=AC，连接DE，

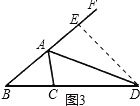
在△ACD和△AED中，

，

∴△ACD≌△AED（SAS），

∴∠ACD=∠AED，CD=DE，

∴∠ACB=∠FED，

又∵∠ACB=2∠B

∴∠FED=2∠B，

又∵∠FED=∠B＋∠EDB，

∴∠EDB=∠B，

∴DE=BE，

∴BE=CD，

∵AB=BE-AE

∴AB=CD﹣AC．