【题目】某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：

请解答以下问题：

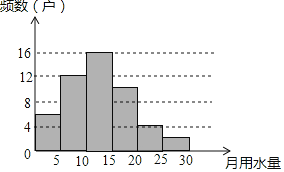
（1）把上面的频数分布表和频数分布直方图补充完整；

（2）若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？

（3）为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？

参考答案：

【答案】（1）见解析；（2）240户；（3）15t.

【解析】

（1）根据月用水量在0≤x<5范围的频数与百分比可得调查的总户数，从而可求得用水量在10≤x＜15的频数以及20≤x＜25的频率，据此补全图、表即可；

（2）用2000乘以月少水量不低于20t的家庭所占的比例即可；

（3）根据各分组的百分比进行判断即可得.

（1）∵被调查的总数量为6÷12%=50（户），

∴10≤x＜15的频数为50×32%=16（户）、20≤x＜25的频率为4÷50=0.08=8%，

补全图形如下：

月均用水量

频数

百分比

0≤x＜5

6

　12%

5≤x＜10

12

　24%

10≤x＜15

16

　32%

15≤x＜20

10

　20%

20≤x＜25

4

8%

25≤x＜30

2

　4%

合计

50

100%

（2）估计该小区月均用水量不低于20t的家庭有2000×（8%+4%）=240户；

（3）∵前三个分组的频率之和为12%+24%+32%=68%，

∴家庭月均用水量应定为15t．

关闭