【题目】如图,直线l上有A、B两点,点O是线段AB上的一点,且OA=10cm,OB=5cm.
(1)若点C是线段 AB 的中点,求线段CO的长.
(2)若动点 P、Q 分别从 A、B 同时出发,向右运动,点P的速度为4cm/s,点Q的速度为3cm/s,设运动时间为 x 秒,
①当 x=__________秒时,PQ=1cm;
②若点M从点O以7cm/s的速度与P、Q两点同时向右运动,是否存在常数m,使得4PM+3OQ﹣mOM为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.
(3)若有两条射线 OC、OD 均从射线OA同时绕点O顺时针方向旋转,OC旋转的速度为6度/秒,OD 旋转的速度为2度/秒.当OC与OD第一次重合时,OC、OD 同时停止旋转,设旋转时间为t秒,当t为何值时,射线 OC⊥OD?

参考答案:
【答案】(1)CO=2.5;(2)①14和16 ;②定值55,理由见解析;(3)t=22.5和67.5
【解析】
(1)先求出线段AB的长,然后根据线段中点的定义解答即可;
(2)①由PQ=1,得到|15-(4x-3x)|=1,解方程即可;
②先表示出PM、OQ、OM的长,代入4PM+3OQ﹣mOM得到55+(21-7m)x,要使4PM+3OQ﹣mOM为定值,则21-7m=0,解方程即可;
(3)分两种情况讨论,画出图形,根据图形列出方程,解方程即可.
(1)∵OA=10cm,OB=5cm,∴AB=OA+OB=15cm.
∵点C是线段 AB 的中点,∴AC=![]() AB=7.5cm,∴CO=AO-AC=10-7.5=2.5(cm).
AB=7.5cm,∴CO=AO-AC=10-7.5=2.5(cm).
(2)①∵PQ=1,∴|15-(4x-3x)|=1,∴|15-x|=1,∴15-x=±1,解得:x=14或16.
②∵PM=10+7x-4x=10+3x,OQ=5+3x,OM=7x,∴4PM+3OQ﹣mOM=4(10+3x)+3(5+3x)-7mx=55+(21-7m)x,要使4PM+3OQ﹣mOM为定值,则21-7m=0,解得:m=3,此时定值为55.
(3)分两种情况讨论:①如图1,根据题意得:6t-2t=90,解得:t=22.5;
②如图2,根据题意得:6t+90=360+2t,解得:t=67.5.
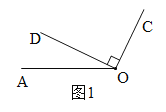
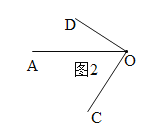
综上所述:当t=22.5秒和67.5秒时,射线 OC⊥OD.
-
科目: 来源: 题型:
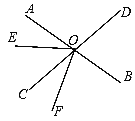
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
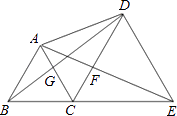
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段长分别为10,14,20,以其中两条为对角线,剩余一条为边,可以画出________个平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年法国网球公开赛中,我国选手李娜在决赛中成功击败对手夺冠,称为获得法国网球公开赛冠军的亚洲第一人.某班体育委员就本班同学对该届法国网球公开赛的了解程度进行全面调查统计,收集数据后绘制了两幅不完整的统计图,如图(1)和图(2).根据图中的信息,解答下列问题:
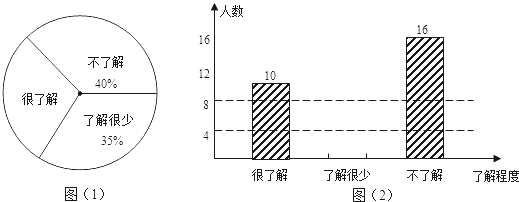
(1)该班共有名学生;
(2)在图(1)中,“很了解”所对应的圆心角的度数为;
(3)把图(2)中的条形图形补充完整. -
科目: 来源: 题型:
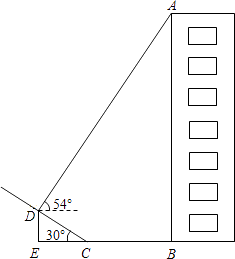
查看答案和解析>>【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段长分别为7,15,20,以其中一条为对角线,另两条为邻边,可以画出________个平行四边形.
相关试题

