【题目】如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD. 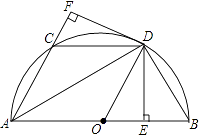
(1)求证:△CDF≌△BDE;
(2)当AD=时,四边形AODC是菱形;
(3)当AD=时,四边形AEDF是正方形.
参考答案:
【答案】
(1)证明:∵弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
∵弦AD平分∠BAC,
∴∠FAD=∠BAD,
∴BD=CD.
在Rt△BED和Rt△CFD中 ![]() ,
,
∴Rt△BED≌Rt△CFD (HL);
(2)![]()
(3)![]() a
a
【解析】解:(2)四边形AODC是菱形时, OD=CD=DB=OB,
∴∠DBA=60°,
∴AD=ABcos∠DBA=asin60°= ![]() a,
a,
故答案为: ![]() ;(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
;(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理,得
AD= ![]() =
= ![]() a,
a,
故答案为: ![]() a.
a.
(1)根据角平分线的性质,可得DF与DE的关系,根据圆周角定理,可得DC与DB的关系,根据HL,可得答案;(2)根据菱形的性质,可得OD与CD,OD与BD的关系,根据正三角形的性质,可得∠DBA的度数,根据三角函数值,可得答案;(3)根据圆周角定理,可得OD⊥AB,根据勾股定理,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50
 ,
,求∠AOC,∠AOF,∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 .
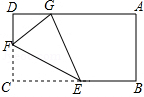
-
科目: 来源: 题型:
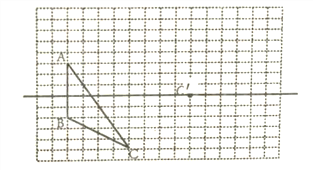
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为l.在方格纸中将三角形ABC经过一次平移后得到三角形A'B'C’,图中标出了点C的对应点C'.
(1)请画出平移后的三角形A'B'C’;
(2)连接AA’,CC’,则这两条线段之间的关系是 ;
(3)建立合适的平面直角坐标系,并写出A'、B'、C'的坐标;
(4)三角形A'B'C'的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:

(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD,分别探究下列四个图形(图①、②、③、④)中∠APC和∠PAB、∠PCD的数量关系,用等式表示出来.

(1)设∠APC=m,∠PAB=n,∠PCD=t.
请用含m,n,t的等式表示四个图形中相应的∠APC和∠PAB、∠PCD的数量关系.(直接写出结果)
图①: ;
图②: ;
图③: ;
图④: .
(2)在(1)中的4个结论中选出一个你喜欢的结论加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1:
 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
相关试题

