【题目】如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 . 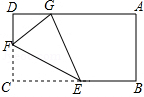
参考答案:
【答案】![]() ≤CF≤3
≤CF≤3
【解析】解:∵四边形ABCD是矩形, ∴∠C=90°,BC=AD=5,CD=AB=3,
当点D与F重合时,CF最大=3,如图1所示: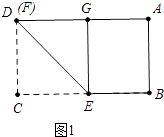
当B与E重合时,CF最小,如图2所示:
在RTABG中,∵BG=BC=5,AB=3,
∴AG= ![]() =4,
=4,
∴DG=AD﹣AG=1,设CF=FG=x,
在RT△DFG中,∵DF2+DG2=FG2 ,
∴(3﹣x)2+12=x2 ,
∴x= ![]() ,
,
∴ ![]() ≤CF≤3.
≤CF≤3.
故答案为 ![]() ≤CF≤3.
≤CF≤3.
当点E与B重合时,CF最小,先利用勾股定理求出AG,设CF=FG=x,在RT△DFG中,利用勾股定理列出方程即可解决问题,.当F与D重合时,CF最大.由此即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45
 ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50
 ,
,求∠AOC,∠AOF,∠EOF的度数.

-
科目: 来源: 题型:
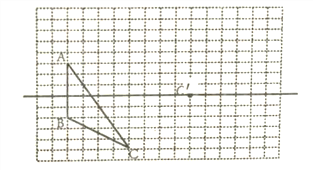
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为l.在方格纸中将三角形ABC经过一次平移后得到三角形A'B'C’,图中标出了点C的对应点C'.
(1)请画出平移后的三角形A'B'C’;
(2)连接AA’,CC’,则这两条线段之间的关系是 ;
(3)建立合适的平面直角坐标系,并写出A'、B'、C'的坐标;
(4)三角形A'B'C'的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
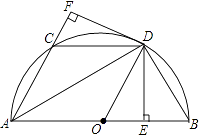
(1)求证:△CDF≌△BDE;
(2)当AD=时,四边形AODC是菱形;
(3)当AD=时,四边形AEDF是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:

(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
相关试题

