搜索
【题目】如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是_______．
参考答案：
【答案】2或5．
【解析】
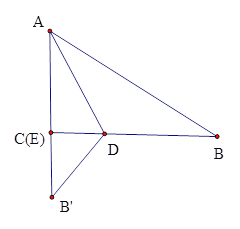
试题在Rt△ABC中，AB=
，①若∠DEB′=90°，即AB′与AC重合 ，见下图．此时B′E=10-6=4，CD+B′D=8，设DB=x，则DE=8-x，∴42+（8-x）2=x2，解得x=5，∴BD=5．
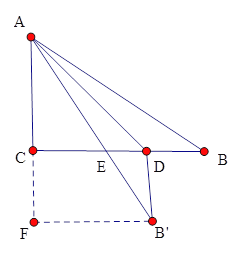
②若∠EDB′=90°，如下图，过点B′作B′F⊥AC交AC延长线与点F．则四边形CDFB′是矩形．∴CF=DB′=DB，B′F=CD，设BD=x，则B′F=8-x，AF=6+x，∴（6+x）2+（8-x）2=102，解得x=2，∴BD=2．综上所述，BD=2或5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两名选手在同等条件下进行射击对抗赛，他们各射靶10次，为了比较两人的成绩，制作了如下统计图表：
甲、乙射击成绩统计表
平均数
众数
中位数
方差
10环次数
甲
8
乙
(1)请补全上述图表(请直接在表中填空和补全折线图)；
(2)如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
(3)如果希望(2)中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：已知方程a2
2a1=0，12bb2=0且ab≠1，求
的值.解：由a2
2a1=0及12bb2=0，可知a≠0，b≠0，
又∵ab≠1，
.1
2bb2=0可变形为
，根据a2
2a1=0和的特征.
、
是方程x22x1=0的两个不相等的实数根，则
，即
.根据阅读材料所提供的方法，完成下面的解答.
已知：3m2
7m2=0，2n2+7n3=0且mn≠1，求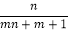
的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】某饮料厂开发了A，B两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A，B两种饮料共100瓶．设生产A种饮料x瓶，解析下列问题：
原料名称
饮料名称甲
乙
A
20克
40克
B
30克
20克
（1）有几种符合题意的生产方案写出解析过程；
（2）如果A种饮料每瓶的成本为2.60元，B种饮料每瓶的成本为2.80元，这两种饮料成本总额为y元，请写出y与x之间的关系式，并说明x取何值会使成本总额最低？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=AC=5，cos∠ABC=0.6，将△ABC绕点C顺时针旋转，得到△A1B1C．
（1）如图1，当点B1在线段BA延长线上时．①求证：BB1∥CA1；②求△AB1C的面积；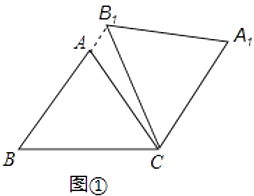
（2）如图2，点E是BC边的中点，点F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F1 ， 求线段EF1长度的最大值与最小值的差．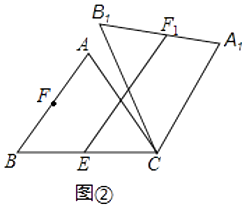
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y1=
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B（0，1）和点C，且图象C′过点A（2﹣ 
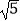，0）．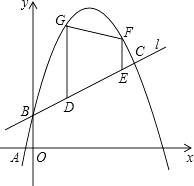
（1）求二次函数的最大值；
（2）设使y2＞y1成立的x取值的所有整数和为s，若s是关于x的方程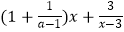
=0的根，求a的值；
（3）若点F、G在图象C′上，长度为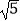 的线段DE在线段BC上移动，EF与DG始终平行于y轴，当四边形DEFG的面积最大时，在x轴上求点P，使PD+PE最小，求出点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD等于（ ）
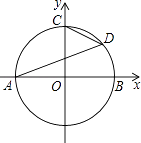
A.20°
B.40°
C.65°
D.70°
相关试题
