【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)根据甲的平均成绩可计算出甲的第6次射击为6环,再根据图表数据可分别求得平均数、众数、中位数、方差和10环次数,补全图表即可;
(2)方差小的成绩稳定;
(3)因为乙选手10环次数较多,所以评判规则可以是10环次数多的胜出.
解:(1)根据射击成绩统计表和折线统计图设甲的第6次射击为x环,得:甲的平均分
![]() ,
,
解得x=6,所以甲的第6次射击为6环.
将甲的射击的环数由小到大的顺序排列为:6,6,7,7,8,9,9,9,9,10.
9环出现的次数为4次最多,所以甲的众数为9,
甲的中位数为![]() (环).
(环).
甲的方差为:![]() ;
;
乙的射击成绩为:6,7,5,8,10,7,8,10,9,10,
则平均数为![]() (环),
(环),
将乙的射击的环数由小到大的顺序排列为:5,6,7,7,8,8,9,10,10,10.
10环出现的次数为3次最多,所以乙的众数为10,
乙的中位数为![]() (环),方差为
(环),方差为
乙的方差为:![]() .
.
(1)补全图表如下:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | 9 | 8.5 | 1.8 | 1 |
乙 | 8 | 10 | 8 | 2.8 | 3 |
甲、乙射击成绩折线图

(2)由于甲的方差小于乙的方差,甲比较稳定,故甲胜出.
(3)如果希望乙胜出,应该制定的评判规则为:如满环(10环)次数多者胜出或众数大的胜出等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)4(3x
 5)2=(x
5)2=(x 4)2;
4)2;(2)y2
 2y
2y 8=0;
8=0;(3)x(x
 3)=4(x
3)=4(x 1) .
1) . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
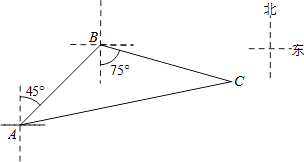
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为三角形的三边,求证:方程a2x2
 (a2+c2
(a2+c2 b2)x+c2=0没有实数根.
b2)x+c2=0没有实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:已知方程a2
 2a
2a 1=0,1
1=0,1 2b
2b b2=0且ab≠1,求
b2=0且ab≠1,求 的值.
的值.解:由a2
 2a
2a 1=0及1
1=0及1 2b
2b b2=0,
b2=0,可知a≠0,b≠0,
又∵ab≠1,
 .
.1
 2b
2b b2=0可变形为
b2=0可变形为 ,
,根据a2
 2a
2a 1=0和
1=0和 的特征.
的特征. 、
、 是方程x2
是方程x2 2x
2x 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,则
 ,即
,即 .
.根据阅读材料所提供的方法,完成下面的解答.
已知:3m2
 7m
7m 2=0,2n2+7n
2=0,2n2+7n 3=0且mn≠1,求
3=0且mn≠1,求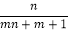 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称
饮料名称甲
乙
A
20克
40克
B
30克
20克
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

相关试题

