【题目】如图,已知一次函数y1= ![]() x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣ ![]() ,0).
,0).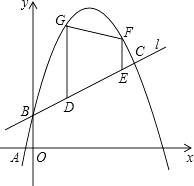
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程 ![]() =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为 ![]() 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
参考答案:
【答案】
(1)解:∵二次函数y2=﹣x2+mx+b经过点B(0,1)与A(2﹣ ![]() ,0),
,0),
∴ ![]() ,
,
解得 ![]()
∴l:y1= ![]() x+1;
x+1;
C′:y2=﹣x2+4x+1.
∵y2=﹣x2+4x+1=﹣(x﹣2)2+5,
∴ymax=5
(2)解:联立y1与y2得: ![]() x+1=﹣x2+4x+1,解得x=0或x=
x+1=﹣x2+4x+1,解得x=0或x= ![]() ,
,
当x= ![]() 时,y1=
时,y1= ![]() ×
× ![]() +1=
+1= ![]() ,
,
∴C( ![]() ,
, ![]() ).
).
使y2>y1成立的x的取值范围为0<x< ![]() ,
,
∴s=1+2+3=6.
代入方程得 ![]()
解得a= ![]() ;
;
经检验a= ![]() 是分式方程的解
是分式方程的解
(3)解:∵点D、E在直线l:y1= ![]() x+1上,
x+1上,
∴设D(p, ![]() p+1),E(q,
p+1),E(q, ![]() q+1),其中q>p>0.
q+1),其中q>p>0.
如答图1,过点E作EH⊥DG于点H,则EH=q﹣p,DH= ![]() (q﹣p).
(q﹣p).

在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q﹣p)2+[ ![]() (q﹣p)]2=(
(q﹣p)]2=( ![]() )2,
)2,
解得q﹣p=2,即q=p+2.
∴EH=2,E(p+2, ![]() p+2).
p+2).
当x=p时,y2=﹣p2+4p+1,
∴G(p,﹣p2+4p+1),
∴DG=(﹣p2+4p+1)﹣( ![]() p+1)=﹣p2+
p+1)=﹣p2+ ![]() p;
p;
当x=p+2时,y2=﹣(p+2)2+4(p+2)+1=﹣p2+5,
∴F(p+2,﹣p2+5),
∴EF=(﹣p2+5)﹣( ![]() p+2)=﹣p2﹣
p+2)=﹣p2﹣ ![]() p+3.
p+3.
S四边形DEFG= ![]() (DG+EF)EH=
(DG+EF)EH= ![]() [(﹣p2+
[(﹣p2+ ![]() p)+(﹣p2﹣
p)+(﹣p2﹣ ![]() p+3)]×2=﹣2p2+3p+3
p+3)]×2=﹣2p2+3p+3
∴当p= ![]() 时,四边形DEFG的面积取得最大值,
时,四边形DEFG的面积取得最大值,
∴D( ![]() ,
, ![]() )、E(
)、E( ![]() ,
, ![]() ).
).
如答图2所示,过点D关于x轴的对称点D′,则D′( ![]() ,﹣
,﹣ ![]() );
);
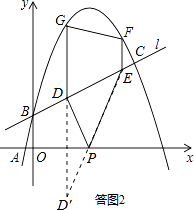
连接D′E,交x轴于点P,PD+PE=PD′+PE=D′E,
由两点之间线段最短可知,此时PD+PE最小.
设直线D′E的解析式为:y=kx+b,
则有 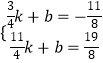 ,
,
解得 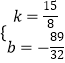
∴直线D′E的解析式为:y= ![]() x﹣
x﹣ ![]() .
.
令y=0,得x= ![]() ,
,
∴P( ![]() ,0).
,0).
【解析】(1)用待定系数法将点B、点A代入一次函数解析式和二次函数解析式,就可以求出两函数的解析式,再求出二次函数的顶点坐标,即可求出函数的最大值。
(2)先求出抛物线与直线BC的两交点坐标,观察图像,写出使y2>y1成立的x的取值范围,求出所有整数的和s的值,再将x=s代入方程,既可求出a的值。注意:此方程式分式方程必须检验。
(3)抓住已知条件中的长度为 5 的线段DE在线段BC上移动,EF与DG始终平行于y轴,因此添加辅助线,过点E作EH⊥DG于点H,D、E两点再直线BC上,设出这两点的坐标,根据勾股定理,得出EH=2,E(p+2,![]() p+2),再将当x=p时,当x=p+2时,分别代入二次函数解析式,求出对应的函数值,即可表示出点F、点G的坐标,再求出DG、EF的长,根据梯形的面积求出s与t的函数关系式,求出顶点坐标,即可求得p的值,并求出点D、E的坐标,要在x轴上求点P,使PD+PE最小,因此过点D作关于x轴的对称点D′,,求出直线D′E的解析式,即可求出点P的坐标
p+2),再将当x=p时,当x=p+2时,分别代入二次函数解析式,求出对应的函数值,即可表示出点F、点G的坐标,再求出DG、EF的长,根据梯形的面积求出s与t的函数关系式,求出顶点坐标,即可求得p的值,并求出点D、E的坐标,要在x轴上求点P,使PD+PE最小,因此过点D作关于x轴的对称点D′,,求出直线D′E的解析式,即可求出点P的坐标
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对二次函数的最值的理解,了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称
饮料名称甲
乙
A
20克
40克
B
30克
20克
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;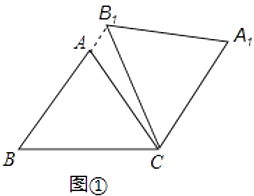
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.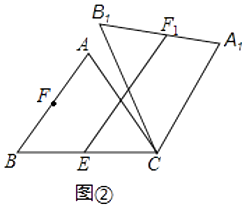
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD等于( )
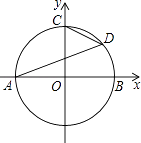
A.20°
B.40°
C.65°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,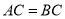 ,若有一动点
,若有一动点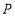 从
从 出发,沿
出发,沿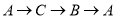 匀速运动,则
匀速运动,则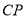 的长度
的长度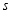 与时间
与时间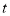 之间的关系用图像表示大致是( )
之间的关系用图像表示大致是( )
A.
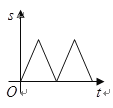 B.
B.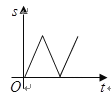
C.
 D.
D.
相关试题

