搜索
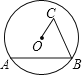
【题目】如图，在圆 O 中有折线 ABCO，BC=6，CO=4，∠B=∠C=60°，则弦 AB 的长为__________________.
参考答案：
【答案】10
【解析】分析：作OD⊥AB垂足为D，利用垂径定理得AB=2BD，作OE∥AB交BC于E，构造等边△COE，过E点作EF⊥AB，垂足为F，得Rt△BEF，而∠B=60°，可得BF=
BE，再根据BD=BF+DF求BD．
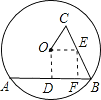
详解：如图，作OD⊥AB垂足为D，OE∥AB交BC于E，过E点作EF⊥AB，垂足为F，
∵OE∥AB，∴△COE为等边三角形，∴OE=CE=OC=4，
∵OD⊥AB，EF⊥AB，∴DF=OE=4，BE=BC-CE=2，
在Rt△BEF中，∵∠B=60°，∴BF=BE=1，
∴BD=BF+DF=1+4=5，
由垂径定理，得AB=2BD=10．
故答案为：10.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明用尺规作图作△ABC边AC上的高BH，作法如下：
①分别以点D，E为圆心，大于
DE的长为半径作弧，两弧交于F； ②作射线BF，交边AC于点H；
③以B为圆心，BK长为半径作弧，交直线AC于点D和E；
④取一点K，使K和B在AC的两侧；
所以，BH就是所求作的高． 其中顺序正确的作图步骤是（ ）
A. ①②③④ B. ④③②① C. ②④③① D. ④③①②
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校召开运动会，七（1）班学生到超市分两次（第二次少于第一次）购买某种饮料90瓶，共用去205元，已知该种饮料价格如下：
购买瓶数/瓶
不超过30
30以上不超过50
50以上
单价/元
3
2.5
2
求：两次分别购买这种饮料多少瓶？
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于一个函数，如果它的自变量 x 与函数值 y 满足：当1≤x≤1 时，1≤y≤1，则称这个函数为“闭 函数”.例如：y=x，y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”，且抛物线经过点 A(1，1)和点 B(1，1)，则 a 的取值范围是______________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小高从家门口骑车去离家4千米的单位上班，先花3分钟走平路1千米，再走上坡路以0.2千米/分钟的速度走了5分钟，最后走下坡路花了4分钟到达工作单位，若设他从家开始去单位的时间为t（分钟），离家的路程为y（千米），则y与t（8<t≤12）的函数关系为（ ）
A. y=0.5t（8<t≤12） B. y=0.5t+2（8<t≤12）
C. y=0.5t+8（8<t≤12） D. y="0." 5t-2（8<t≤12）
-
科目： 来源： 题型：
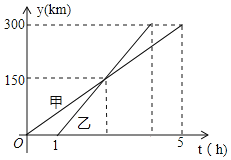
查看答案和解析>>【题目】甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y（km）与行驶的时间t（h）之间的函数关系如图所示．
（1）求乙车离开A城的距离y关于t的函数解析式；
（2）求乙车的速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当前，交通拥堵是城市管理的一大难题．我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用，但为了保证安全，高架桥上最高限速 80 千米/小时．在一般条件下，高架桥上的车流 速度 v（单位：千米/小时）是车流密度 x（单位：辆/千米）的函数，当桥上的车流密度达到 180 辆/千 米时，造成堵塞，此时车流速度为 0；当 0≤x≤20 时，桥上畅通无阻，车流速度都为 80 千米/小时， 研究表明：当 20≤x≤180 时，车流速度 v 是车流密度 x 的一次函数．
（1）当 0≤x≤20 和 20≤x≤180 时，分别写出函数 v 关于 x 的函数关系式；
（2）当车流密度 x 为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）w=x·v可以达到最大，并求出最大值；
（3）某天早高峰（7:30—9:30）经交警部门控制管理，桥上的车流速度始终保持 40 千米/小时，问这天 早高峰期间高架桥分流了多少辆车?
相关试题
