【题目】如图,已知⊙O的半径长为R=5,弦AB 与弦CD平行,他们之间距离为7,AB=6求:弦CD的长.
参考答案:
【答案】过O向AB作垂线,垂足为E , 根据垂径定理可以得到AE=3,连接OA , 在直角三角形AOE中,根据勾股定理可以得到OE= ![]() .同样过O点想CD作垂线,垂足为F , 因为弦AB和弦CD之间的距离为7,那么OF=3,连接OC , 在直角三角形OCF中CF=
.同样过O点想CD作垂线,垂足为F , 因为弦AB和弦CD之间的距离为7,那么OF=3,连接OC , 在直角三角形OCF中CF= ![]() ,根据垂径定理可以知道点F为CD的中点,即CD=8.
,根据垂径定理可以知道点F为CD的中点,即CD=8.
【解析】此题考查了垂径定理和勾股定理知识点.
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
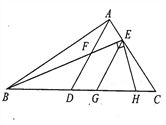
查看答案和解析>>【题目】如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E、F分别是AB、AC、BC的中点,
(1)若EF=10cm,则AB= cm;若BC=20cm,则DE= cm;
(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
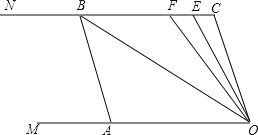
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
-
科目: 来源: 题型:
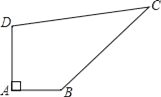
查看答案和解析>>【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系中,已知点P(-2,-1),点T(t , 0)是x轴上的一个动点.

(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
相关试题

