【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴∠FAB=∠ABE=90°,AF∥BE,
∵EF⊥AD,
∴∠FAB=∠ABE=∠AFE=90°,
∴四边形ABEF是矩形,
∵AE平分∠BAD,AF∥BE,
∴∠FAE=∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是正方形;
(2)解:过点P作PH⊥AD于H,如图所示:

∵四边形ABEF是正方形,
∴BP=PF,BA⊥AD,∠PAF=45°,
∴AB∥PH,
∵AB=6,
∴AH=PH=3,
∵AD=8,
∴DH=AD﹣AH=8﹣3=5,
在Rt△PHD中,∠PHD=90°.
∴tan∠ADP= ![]() =
= ![]() .
.
【解析】(1)先根据有一角为直角的平行四边形是矩形证四边形ABEF是矩形,然后再证AB=BE,可得证;
(2)过点P作PH⊥AD于H,根据四边形ABEF是正方形和已知,易求出DH、PH的长,再在在Rt△PHD中,利用三角函数的定义可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣
 )﹣2﹣|﹣
)﹣2﹣|﹣ 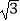 |+2sin60°+(π﹣4)0 .
|+2sin60°+(π﹣4)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图,若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%

根据图表中提供的信息,解答下列问题:
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳. -
科目: 来源: 题型:
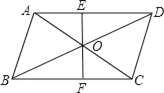
查看答案和解析>>【题目】如图平行四边形ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC分别交于点E,F,已知AE=3,BF=5
(1)求BC的长;
(2)如果两条对角线长的和是20,求三角形△AOD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

相关试题

