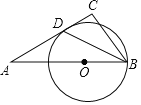
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
连接OD,得Rt△OAD,由∠A=30°,AD=2![]() ,可求出OD、AO的长;由BD平分∠ABC,OB=OD可得OD 与BC间的位置关系,根据平行线分线段成比例定理,得结论.
,可求出OD、AO的长;由BD平分∠ABC,OB=OD可得OD 与BC间的位置关系,根据平行线分线段成比例定理,得结论.
连接OD

∵OD是⊙O的半径,AC是⊙O的切线,点D是切点,
∴OD⊥AC
在Rt△AOD中,∵∠A=30°,AD=2![]() ,
,
∴OD=OB=2,AO=4,
∴∠ODB=∠OBD,又∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥CB,
∴![]() ,即
,即![]() ,
,
∴CD=![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B.
 cm C. 2.5cm D.
cm C. 2.5cm D.  cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图(1),已知:在三角形
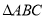 中,
中,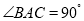 ,
,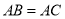 ,直线
,直线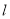 经过点
经过点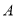 ,
,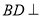 直线
直线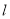 ,
,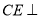 直线
直线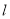 ,垂足分别为点
,垂足分别为点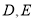 ,试写出线段
,试写出线段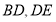 和
和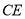 之间的数量关系为_________________.
之间的数量关系为_________________.(2)思考探究:如图(2),将图(1)中的条件改为:在
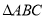 中,
中, 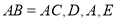 三点都在直线
三点都在直线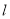 上,并且
上,并且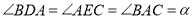 ,其中
,其中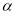 为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图(3),
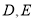 是
是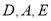 三点所在直线
三点所在直线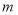 上的两动点,(
上的两动点,(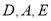 三点互不重合),点
三点互不重合),点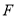 为
为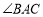 平分线上的一点,且
平分线上的一点,且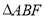 与
与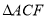 均为等边三角形,连接
均为等边三角形,连接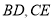 ,若
,若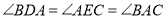 ,试判断
,试判断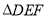 的形状并说明理由.
的形状并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
 城出发匀速行驶至
城出发匀速行驶至 城.在整个行驶过程中,甲、乙两车离
城.在整个行驶过程中,甲、乙两车离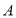 城的距离
城的距离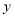 (千米)与甲车行驶的时间
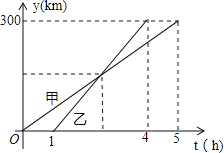
(千米)与甲车行驶的时间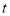 (小时)之间的函数关系如图所示.则下列结论:
(小时)之间的函数关系如图所示.则下列结论:①
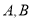 两城相距
两城相距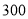 千米;
千米;②乙车比甲车晚出发
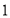 小时,却早到
小时,却早到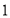 小时;
小时;③乙车出发后
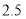 小时追上甲车;
小时追上甲车;④当甲、乙两车相距
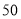 千米时,
千米时,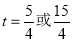
其中正确的结论有( )
A.
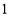 个B.
个B.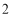 个C.
个C.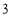 个D.
个D.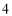 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
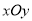 中,矩形
中,矩形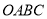 如图放置,动点
如图放置,动点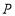 从
从 出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成
出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成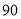 度角(反弹后仍在矩形内作直线运动),当点
度角(反弹后仍在矩形内作直线运动),当点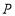 第
第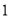 次碰到矩形的边时,点
次碰到矩形的边时,点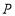 的坐标为
的坐标为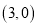 ;当点
;当点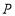 第
第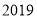 次碰到矩形的边时,点
次碰到矩形的边时,点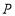 的坐标为 __________.
的坐标为 __________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式.
相关试题

