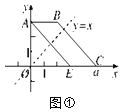
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
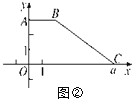
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
参考答案:
【答案】(1)点E的坐标为(3,0);(2) a=5;(3) y=![]() x或y=
x或y=![]() x.
x.
【解析】
(1)由折叠的性质可知OE=OA,由OA的长即可确定出点E的坐标;
(2)①由平行四边形的性质可知EC=AB,结合OE的长即可求得a的值;
②根据梯形的面积公式以及梯形的面积可求得a的值,从而可求得梯形的面积,设直线y=mx交BC于点D,点D的坐标为(xD,yD),由直线y=mx将梯形面积分为1∶2两部分,可得S△OCD=4或S△OCD=8,然后根据三角形的面积公式求得yD=![]() 或yD=
或yD=![]() ,利用待定系数法可得直线BC的函数表达式,将yD分别代入即可求得直线y=mx的解析式.
,利用待定系数法可得直线BC的函数表达式,将yD分别代入即可求得直线y=mx的解析式.
(1)由折叠的性质可知OE=OA,
∵A(0,3),∴OA=3,
∴OE=3,
∴点E的坐标为(3,0);
(2)∵BC∥AE,AB∥CE,∴四边形ABCE是平行四边形,
∴CE=AB=2,∴OC=OE+CE=5,
∴a=5;
(3)S梯形ABCO=![]() (AB+OC)·AO=2a,即
(AB+OC)·AO=2a,即![]() ,解得a=6,
,解得a=6,
∴S梯形ABCO=12,
设直线y=mx交BC于点D,点D的坐标为(xD,yD),
∵直线y=mx将梯形面积分为1∶2两部分,
∴S△OCD=![]() ×12=4或S△OCD=
×12=4或S△OCD=![]() ×12=8,
×12=8,
当S△OCD=4时,![]() ×6yD=4,解得yD=
×6yD=4,解得yD=![]() ,
,
当S△OCD=8时,![]() ×6yD=8,解得yD=
×6yD=8,解得yD=![]() ,
,
由B(2,3),C(6,0),可得直线BC的函数表达式为y=-![]() x+
x+![]() ,
,
则当yD=![]() 时,xD=
时,xD=![]() ,此时y=
,此时y=![]() x;
x;
当yD=![]() 时,xD=
时,xD=![]() ,此时y=
,此时y=![]() x,
x,
综上可知y=![]() x或y=
x或y=![]() x.
x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=
 x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.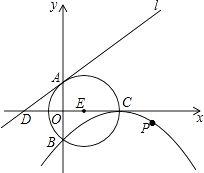
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A在函数
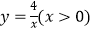 的图象上,AB⊥
的图象上,AB⊥ 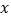 轴于点B,AB的垂直平分线与
轴于点B,AB的垂直平分线与 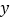 轴交于点C,与函数
轴交于点C,与函数 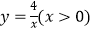 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )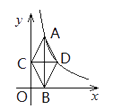
A. 2
B.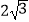
C.4
D.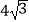
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
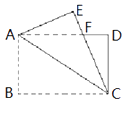
A.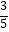
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
相关试题

