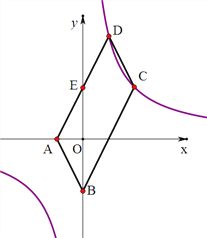
【题目】如图1,已知点A(﹣2,0),点B(0,﹣4),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,8)、C(4,b).
经过C,D两点且D(a,8)、C(4,b).
(1)求a、b、k的值;
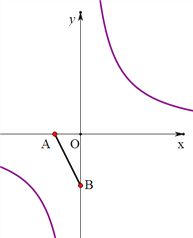
(2)如图2,点P在双曲线y=![]() 上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
参考答案:
【答案】(1) a=2,k=16,b=4;(2) Q1(6,0)或Q1(-6,0)Q1(2,0).
【解析】分析:
(1)如下图,过点D作DP⊥y轴于点P,结合已知条件可证得△PDE≌△OAE,由此可得PD==a=OA=2,这样即可得到点D的坐标,将点D的坐标代入![]() 中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
(2)如下图,分AB为所求平行四边形的边和对角线两种情况结合已知条件分析讨论即可.
(1)如图1,过点D作DP⊥y轴于点P,
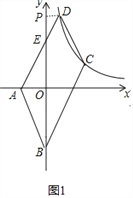
∵点E为AD的中点,
∴AE=DE.
又∵DP⊥y轴,∠AOE=90°,
∴∠DPE=∠AEO.
∵在△PDE与△OAE中,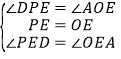 ,
,
∴△PDE≌△OAE(ASA),
∴PD=OA,
∵A(﹣2,0),
∴a=2,
∴D(2,8).
∵点D在反比例函数图象上,
∴k=xy=2×8=16.
∵点C在反比例函数图象上,C的坐标为(4,b),
∴b=![]() =4,
=4,
∴a=2,k=16,b=4;
(2)∵点P在双曲线![]() 上,点Q在x轴上,
上,点Q在x轴上,
∴可设点P的坐标为![]() ,点Q的坐标为(m,0),
,点Q的坐标为(m,0),
如下图,①当AB为所求平行四边形ABP1Q1的边时,由点B的坐标为(0,-4)可得点P此时的坐标(-4,-4),∴PB=AQ1=4,
∴OQ1=OA+AQ1=6,
∴此时点Q1的坐标为(-6,0);
②当AB为所求平行四边形ABQ2P2的边时,由平行四边形的性质可知点P到x轴的距离=点B到x轴的距离=4,
∴点P此时的坐标为(4,4);
又∵点P可以可知是由点A平移得到的,而点Q2可以看着是由点B平移得到的,
∴由平移的性质可得点Q2的坐标为(6,0);
③当AB为所求平行四边形AP1BQ3的对角线时,由AQ3=PB结合①中所得PB=4可得AQ3=4,
∵AO=2,
∴OQ3=4-2=2,
∴Q3的坐标为(2,0);
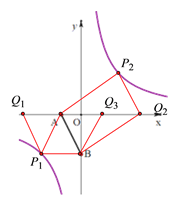
综上所述,满足条件的点Q有3个,坐标分别为:Q1(-6,0)或Q2(6,0)或Q3(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
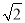 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此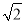 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用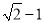 来表示
来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为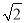 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<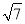 <3,∴
<3,∴ 的整数部分为2,小数部分为
的整数部分为2,小数部分为 ﹣2.
﹣2.请解答:
(1)
 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
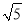 的小数部分为a,
的小数部分为a, 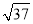 的整数部分为b,求a+b-
的整数部分为b,求a+b-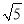 的值;
的值;(3)已知:x是3+
 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
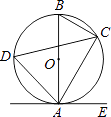
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.
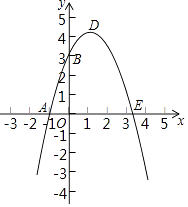
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出P点的坐标,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,AB=5,AD=8,∠A=60°,点P为AD边上任意一点,连接PB,并将PB绕点P逆时针旋转90°得到线段PB′.
(1)当∠DP B′=20°时,∠ABP=____________;
(2)如图2,连结BB′,点P从A运动到D的过程中,求△PBB′面积的取值范围;
(3)若点B′恰好落在
 ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)
ABCD边AD或BC所在的直线上时,直接写出AP的长.(结果保留根号,不必化简)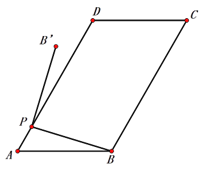
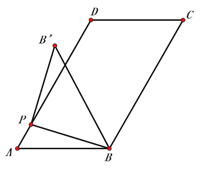
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;
③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( )
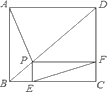
A. ①② B. ①④ C. ①②④ D. ①③④
相关试题

