【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
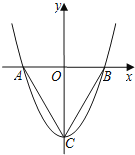
(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
参考答案:
【答案】(1)∠ABC=60°;(2)D (![]() ,
,![]() ).(3)O′(﹣
).(3)O′(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)通过求函数解析式,求出相应线段的长度,观察AC=2OA,进而求出∠ABC度数;
(2)通过观察三角形ADC面积与三角形AOC面积相等,可以判断直线OD∥AC,求出直线与抛物线交点即为点D;
(3)利用抛物线解析式设出O′,通过旋转60°,求出点B′的坐标,将点B′代入抛物线解析式即可求出.
解:(1)由题意与y轴交于点C(0,﹣3),
∴得解析式为y=x2﹣3,
令y=0,x=±![]() ,
,
∴B(![]() ,0),A(﹣
,0),A(﹣![]() ,0),
,0),
∴OA=![]() ,OC=3,AC=2
,OC=3,AC=2![]() ,
,
∴∠OCA=30°,
∴∠ABC=60°;
(2)由(1)得:OA=![]() ,OC=3,
,OC=3,
∴S△OAC=![]() ×3×
×3×![]() =
=![]() ,
,
过原点与AC平行的直线y=﹣![]() ,
,
直线与抛物线的交点即为点D,
联立:![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴D (![]() ,
,![]() ).
).
(3)设点O′(m,m2﹣3),
∵顺时针旋转60°,
则点B′(m+![]() ,m2﹣
,m2﹣![]() ),
),
∴(m+![]() )﹣3=m2﹣
)﹣3=m2﹣![]() ,
,
∴m=﹣![]() ,
,
∴O′(﹣![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a+4b=7ab B.(ab3)3=ab6 C.(a+2)2=a2+4 D.x12÷x6=x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个)
…
30
50
…
销售量y (万个)
…
5
3
…
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△+△=*,○+○=◆,△=○+○+○+○,那么*+◆= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=
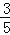 .
.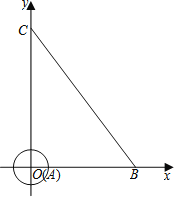
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

相关试题

