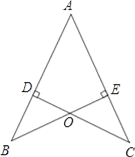
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
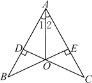
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
先根据角平分线性质可得到OD=OE,根据垂直的定义得到∠BDO=∠CEO=90°,则可利用“ASA”判断△BDO≌△CEO,可得∠B=∠C;根据AAS可证△ABO≌△ACO;根据HL也可证△ADO≌△AEO,可得AD=AE;然后根据AAS,可证△ADC≌△AEB.
∵CD⊥AB,BE⊥AC,∠1=∠2,
∴OD=OE,∠BDO=∠CEO=90°,
在△BDO和△CEO中

∴△BDO≌△CEO(ASA),
∴∠B=∠C.
同理,根据全等三角形的判定:
由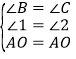
得△ABO≌△ACO(AAS);
由![]()
得Rt△ADO≌Rt△AEO(HL);
由
得△ADC≌△AEB(AAS).
所以,共有4对全等三角形.
故选:D
-
科目: 来源: 题型:
查看答案和解析>>【题目】耐心算一算:
(1)﹣3﹣7;
(2)﹣(﹣7)﹣(﹣5)+(﹣4)
(3)
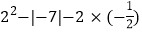
(4)(﹣81)÷
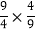 ÷(﹣16)
÷(﹣16)(5)
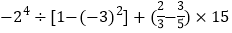
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

-
科目: 来源: 题型:
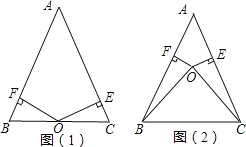
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
答:我抽取的2张卡片是 、 ,乘积的最大值为 .
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
答:我抽取的2张卡片是 、 ,商的最小值为 .
(3)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子.(写出一种即可)
答:我抽取的4张卡片是 、 、 、 ,
算24的式子为 .
相关试题

