【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
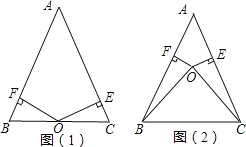
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.
参考答案:
【答案】见解析
【解析】
试题分析:(1)先利用斜边直角边定理证明△OEC和△OFB全等,根据全等三角形对应角相等得到∠B=∠C,再根据等角对等边的性质即可得到AB=AC;
(2)过O作OE⊥AB,OF⊥AC,与(1)的证明思路基本相同.
证明:(1)在Rt△OEC和Rt△OFB中
∵![]() ,
,
∴Rt△OEC≌Rt△OFB(HL),
∴∠B=∠C(全等三角形的对应角相等),
∴AB=AC(等角对等边);
(2)在Rt△OEC和Rt△OFB中,
∵![]() ,
,
∴Rt△OEC≌Rt△OFB(HL),
∴∠OBF=∠OCE,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠FBO+∠OBC=∠OCE+∠OCB,即∠ABC=∠ACB,
∴AB=AC.
-
科目: 来源: 题型:
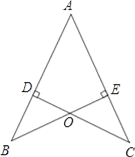
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

-
科目: 来源: 题型:
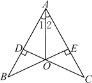
查看答案和解析>>【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
答:我抽取的2张卡片是 、 ,乘积的最大值为 .
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
答:我抽取的2张卡片是 、 ,商的最小值为 .
(3)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子.(写出一种即可)
答:我抽取的4张卡片是 、 、 、 ,
算24的式子为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为2014(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
相关试题

