【题目】在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
参考答案:
【答案】(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
【解析】
(1)根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标即可求出a值;
(3)设AB与y轴交与点D,将x=0代入直线AB的解析式中求出点D的坐标,再根据S△AOP=S△AOD+S△POD利用三角形的面积公式即可得出结论.
解:(1)设直线AB的函数表达式为y=kx+b,把点A、B的坐标代入得:![]() ,
,
解得:k=﹣2,b=3,所以直线AB的函数解析式为y=﹣2x+3;
(2)把P(2,a)代入y=﹣2x+3得:a=﹣1;
(3)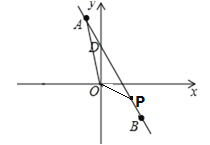
∵把x=0代入y=﹣2x+3得:y=3,
∴直线y=﹣2x+3与y轴的交点为(0,3),即OD=3,
∵P(2,﹣1),
∴△AOP的面积=△AOD的面积+△DOP的面积=![]() +
+![]() =4.5.
=4.5.
故答案为:(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案。
-
科目: 来源: 题型:
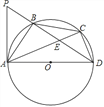
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB=BC.AD是⊙O的直径,AC、BD交于点E,P为DB延长线上一点,且PB=BE.
(1)求证:△ABE∽△DBA;
(2)试判断PA与⊙O的位置关系,并说明理由;
(3)若E为BD的中点,求tan∠ADC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且
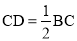 ,联结CM、DN.
,联结CM、DN.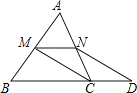
(1)求证:四边形MCDN是平行四边形;
(2)若三角形AMN的面积等于5,求梯形MBDN的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,2)两点,且与x轴交于A点.
(1)求A点坐标;
(2)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值;
(3)在(2)的条件下,在坐标平面内是否还存在一点N,使M,N,A,Q四点恰好构成平行四边形,若存在请求出点N的坐标,若不存在请说明理由。
相关试题

