【题目】定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”.
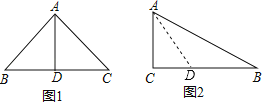
(1)判断(对的打“√”,错的打“×”)
①等边三角形存在“和谐分割线”( )
②如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”( )
(2)如图2,Rt△ABC,∠C=90°,∠B=30°,BC=6,请用尺规画出“和谐分割线”,并计算“和谐分割线”的长度.
参考答案:
【答案】(1)①×,②√;(2)和谐分割线”的长度为4.
【解析】
(1)根据“和谐分割线”的定义即可判断;
(2)如图作∠CAB的平分线,只要证明线段AD是“和谐分割线”即可,并根据直角三角形30°角所对边是斜边的一半和CD+BD=BC=6,求出CD的长度即可.
(1)①因为过等边三角形任意一顶点,分割的两个三角形都有一个角小于60°,即不可能是等边三角形,故等边三角形不存在“和谐分割线”,不正确,是假命题;
②如果三角形中有一个角是另一个角的两倍,
则这个三角形必存在“和谐分割线”,理由如下:
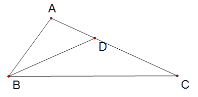
如图,在△ABC中,∠ABC=2∠C,作∠ABC的平分线交AC于D.
∵BD平分∠ABC
∴∠ABD=∠DBC=![]() ,
,
∵∠ABC=2∠C
∴∠ABD=∠DBC=∠C,
∴BD=DC,△BDC为等腰三角形
∠ADB=∠DBC+∠C=2∠C=∠ABC.
故BD为△ABC的和谐分割线.
正确,是真命题,
故答案为:×,√;
(2)如图2,作∠CAB的平分线AD,
∵∠C=90°,∠B=30°,
∴∠DAB=∠B=30°,
∴DA=DB,
∴△ADB是等腰三角形,且∠CAD=∠DAB=∠B,
∴∠ADC=∠B+∠BAD=∠CAD+∠BAD=∠BAC
∴线段AD是△ABC的“和谐分割线”,
设CD=x,则BD=6﹣x,
∵![]() ,
,
∴x=2,
即AD=BD=6﹣2=4;
即和谐分割线”的长度为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=2S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )

A. ①②③ B. ②③ C. ①④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
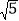 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+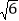 .其中正确结论的序号是( )
.其中正确结论的序号是( )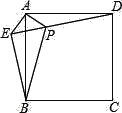
A. ①②③ B. ①②④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为( )

A.80°B.70°C.60°D.50°
相关试题

