【题目】如图,△ABC 是边长为 4 的等边三角形,点 D 是 AB 上异 于 A,B 的一动点,将△ACD 绕点 C 逆时针旋转 60°得△BCE, 则旋转过程中△BDE 周长的最小值_________.

参考答案:
【答案】2![]() +4.
+4.
【解析】
根据旋转的性质可得∠DCE=60°、DC=EC、BE=AD,根据有一个角等于60°的等腰三角形是等边三角形,可判定△CDE是等边三角形,即可得DE=CD,由此计算△DBE的周长=BE+DB+DE=AB+DE=4+DE= CD+4,由垂线段最短可知当CD⊥AB时,△BDE的周长最小,求得CD的长,即可求得△BDE 周长的最小值.
∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
∴DE=CD,
由旋转的性质得,BE=AD,
∴△DBE的周长=BE+DB+DE=AB+DE=4+DE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,CD=2![]() ,
,
∴△BDE的最小周长=CD+4=2![]() +4.
+4.
故答案为:2![]() +4.
+4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
①EF=BE+CF;②∠BGC=90°+
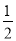 ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则S△AEF=
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则S△AEF=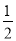 mn.其中正确的结论有( )
mn.其中正确的结论有( )
A.①②④B.①③④C.①②③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△
 C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△ ;
;(2)若将△
 C绕某一点旋转可以得到△
C绕某一点旋转可以得到△ ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;(3)在
 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店某几种型号的计算器每只进价 12 元、售价 20 元,多买优惠, 优惠方法是:凡是一次买 10 只以上的,每多买一只,所买的全部计算器每只就 降价 0.1 元,例如:某人买 18 只计算器,于是每只降价 0.1×(18-10)=0.8(元), 因此所买的 18 只计算器都按每只 19.2 元的价格购买,但是每只计算器的最低售 价为 16 元.
(1)求一次至少购买多少只计算器,才能以最低售价购买? (2)写出该文具店一次销售 x(x>10)只时,所获利润 y(元)与 x(只)之间的函数关系 式,并写出自变量 x 的取值范围;
(3)一天,甲顾客购买了 46 只,乙顾客购买了 50 只,店主发现卖 46 只赚的钱反 而比卖 50 只赚的钱多,请你说明发生这一现象的原因;当 10<x≤50 时,为了 获得最大利润,店家一次应卖多少只?这时的售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为 1 的正方形组成的网格中,△ ABC的顶点均在格点上,A(3,2), B(4, 3), C(1, 1)

(1)画出△ABC关于y轴对称的图形△ A′B′C′
(2)写出A′、B′、C′的坐标(直接写出答案) A′ ;B′ ;C′ ;
(3)写出△ A′B′C′的面积为 .(直接写出答案)
相关试题

