Question

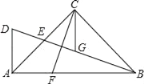
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，F为AB边上﹣点，连接CF，且∠ACF=∠CBG．

（1）求证：AF=CG；

（2）写出图中长度等于2DE的所有线段．

Answer 1

【答案】（1）详见解析；（2）长度等于2DE的线段有CF、BG、DG．

【解析】

（1）要证AF=CG，只需证明△AFC≌△CBG即可．
（2）延长CG交AB于H，则CH⊥AB，H平分AB，继而证得CH∥AD，得出DG=BG和△ADE与△CGE全等，从而证得CF=2DE．

证明：（1）∵∠ACB=90°，CG平分∠ACB，

∴∠ACG=∠BCG=45°，

又∵∠ACB=90°，AC=BC，

∴∠CAF=∠CBF=45°，

∴∠CAF=∠BCG，

在△AFC与△CGB中，

，

∴△AFC≌△CBG（ASA），

∴AF=CG；

（2）延长CG交AB于H，

∵CG平分∠ACB，AC=BC，

∴CH⊥AB，CH平分AB，

∵AD⊥AB，

∴AD∥CG，

∴∠D=∠EGC，

在△ADE与△CGE中，

，

∴△ADE≌△CGE（AAS），

∴DE=GE，

即DG=2DE，

∵AD∥CG，CH平分AB，

∴DG=BG，

∵△AFC≌△CBG，

∴CF=BG，

∴CF=2DE．

∵BG=CF，

∴BG=2DE，

∴DG=2DE，

故长度等于2DE的线段有CF、BG、DG．