【题目】直线y=﹣x+6与x轴交于A,与y轴交于B,直线CD与y轴交于C(0,2)与直线AB交于D,过D作DE⊥x轴于E(3,0).
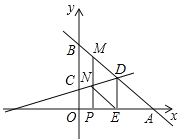
(1)求直线CD的函数解析式;
(2)P是线段OA上一动点,点P从原点O开始,每秒一个单位长度的速度向A运动(P与O,A不重合),过P作x轴的垂线,分别与直线AB,CD交于M,N,设MN的长为S,P点运动的时间为t,求出S与t之间的函数关系式(写出自变量的取值范围)
(3)在(2)的条件下,当t为何值时,以M,N,E,D为顶点的四边形是平行四边形.(直接写出结果)
参考答案:
【答案】(1)y= ![]() x+2;(2)MN=|﹣
x+2;(2)MN=|﹣ ![]() +4|(0<t<6)(3)
+4|(0<t<6)(3)![]() 或
或 ![]() .
.
【解析】(1)由条件可先求得D点坐标,再利用待定系数法可求得直线CD的函数解析式;
(2)用t可分别表示出M、N的坐标,则可表示出S与t之间的关系式;
(3)由条件可知MN∥DE,利用平行四边形的性质可知MN=DE,由(2)的关系式可得到关于t的方程,可求得t的值.
(1)∵直线CD与y轴相交于(0,2),∴可设直线CD解析式为y=kx+2,把x=3代入y=﹣x+6中可得:y=3,∴D(3,3),把D点坐标代入y=kx+2中可得3=3k+2,解得:k=![]() ,∴直线CD的函数解析式为y=
,∴直线CD的函数解析式为y=![]() x+2;
x+2;
(2)由题意可知OP=t,把x=t代入y=﹣x+6中可得:y=﹣t+6,∴M(t,﹣t+6),把x=t代入y=![]() x+2中可得:y=
x+2中可得:y=![]() t+2,∴N(t,
t+2,∴N(t,![]() t+2),∴MN=|﹣t+6﹣(
t+2),∴MN=|﹣t+6﹣(![]() t+2)|=|﹣
t+2)|=|﹣![]() +4|.
+4|.
∵点P在线段OA上,且A(6,0),∴0<t<6,∴MN=|﹣ ![]() +4|(0<t<6);
+4|(0<t<6);
(3)由题意可知MN∥DE.
∵以M,N,E,D为顶点的四边形是平行四边形,∴MN=DE=3,∴|﹣![]() +4|=3,解得:t=
+4|=3,解得:t=![]() 或t=
或t=![]() .
.
即当t的值为![]() 或
或![]() 时,以M,N,E,D为顶点的四边形是平行四边形.
时,以M,N,E,D为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
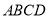 中,
中,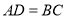 ,
,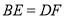 ,
,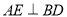 ,
,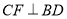 ,垂足分别为
,垂足分别为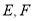 ,则四边形
,则四边形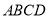 一定是( )
一定是( )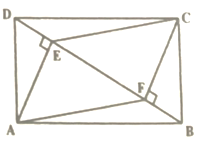
A. 正方形B. 菱形C. 平行四边形D. 矩形
-
科目: 来源: 题型:
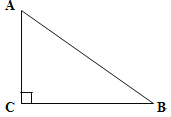
查看答案和解析>>【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,过点
中,过点 的直线交
的直线交 轴正半轴于点
轴正半轴于点 ,将直线
,将直线 绕着点
绕着点 顺时针旋转
顺时针旋转 后,分别与
后,分别与 轴
轴 轴交于点
轴交于点 、
、 .
.(1)若
 ,求直线
,求直线 的函数关系式;
的函数关系式;(2)连接
 ,若
,若 的面积是5,求点
的面积是5,求点 的运动路径长.
的运动路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60
 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120 海里。
海里。
(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:
 =1.41,
=1.41, =1.73,
=1.73, =2.45)
=2.45) -
科目: 来源: 题型:
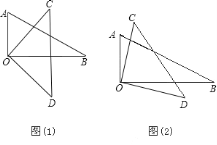
查看答案和解析>>【题目】把一副三角板的直角顶点O重叠在一起,
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
-
科目: 来源: 题型:
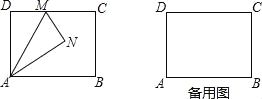
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
相关试题

