【题目】如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
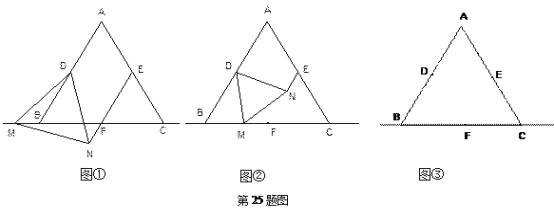
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
参考答案:
【答案】(1)EN与MF相等 (或EN=MF),点F在直线NE上
(2)成立
(3)略
【解析】
(1)判断:EN与MF相等 (或EN=MF),点F在直线NE上,
(2)成立.
证明:
法一:连结DE,DF.
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点,
∴DE,DF,EF为三角形的中位线.∴DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°, ∠NDE+∠FDN=60°,
∴∠MDF=∠NDE.
在△DMF和△DNE中,DF=DE,DM=DN, ∠MDF=∠NDE,
∴△DMF≌△DNE.
∴MF=NE.
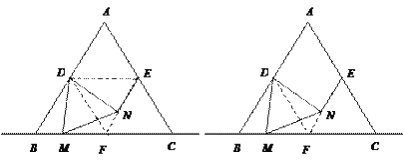
法二:
延长EN,则EN过点F.
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点, ∴EF=DF=BF.
∵∠BDM+∠MDF=60°, ∠FDN+∠MDF=60°,
∴∠BDM=∠FDN.
又∵DM=DN, ∠ABM=∠DFN=60°,
∴△DBM≌△DFN.
∴BM=FN.
∵BF=EF, ∴MF=EN.
法三:
连结DF,NF.
∵△ABC是等边三角形,
∴AC=BC=AC.
又∵D,E,F是三边的中点,
∴DF为三角形的中位线,∴DF=![]() AC=
AC=![]() AB=DB.
AB=DB.
又∠BDM+∠MDF=60°, ∠NDF+∠MDF=60°,
∴∠BDM=∠FDN.
在△DBM和△DFN中,DF=DB,
DM=DN, ∠BDM=∠NDF,∴△DBM≌△DFN.
∴∠B=∠DFN=60°.
又∵△DEF是△ABC各边中点所构成的三角形,
∴∠DFE=60°.
∴可得点N在EF上,
∴MF=EN.
(3)画出图形(连出线段NE),
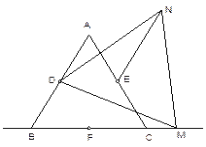
MF与EN相等的结论仍然成立(或MF=NE成立).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.

-
科目: 来源: 题型:
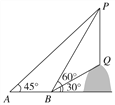
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度(精确到0.1 m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈
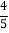 ,cos53°≈
,cos53°≈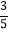 ,tan53°≈ 4 ,
,tan53°≈ 4 ,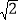 1.41 )
1.41 )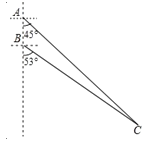
-
科目: 来源: 题型:
查看答案和解析>>【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图4所示).已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上.求点E与点F之间的距离(计算结果精确到0.1 m,参考数据:
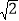 ≈1.41,
≈1.41,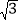 ≈1.73).
≈1.73).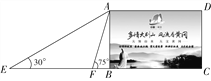
-
科目: 来源: 题型:
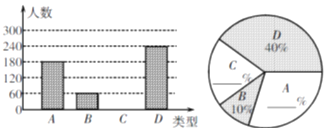
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
相关试题

