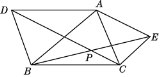
【题目】如图所示,在△ABC外作△ABD和△ACE,使AD=AB,AE=AC,且∠DAB=∠EAC,连接BE,CD相交于P点,求证:点A在∠DPE的平分线上.
参考答案:
【答案】见解析
【解析】
如图,过A点作AM⊥CD于点M,作AN⊥BE于点N,先通过“边角边”证明△BAE≌△DAC,
得到BE=DC,S△BAE=S△DAC,然后通过三角形面积公式得到AN=AM,即得证.
证明:如图,过A点作AM⊥CD于点M,作AN⊥BE于点N,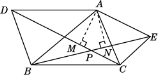
∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,
在△BAE和△DAC中,
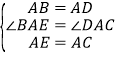 ,
,
∴△BAE≌△DAC(SAS),
∴BE=DC,S△BAE=S△DAC,
∵AM⊥CD,AN⊥BE,
∴![]() BE·AN=
BE·AN=![]() CD·AM,
CD·AM,
∴AN=AM,
∴点A在∠DPE的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图案是由六个全等的直角三角形组成,点O是该图案的中心,则该图案可看成由一个直角三角形绕O点顺时针依次旋转________得到,或可看成由两个相邻的直角三角形绕O点顺时针依次旋转________得到,或可看成由三个相邻的直角三角形绕O点旋转________得到.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为一工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
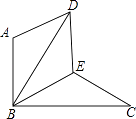
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.

(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
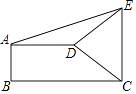
查看答案和解析>>【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3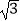
④∠AOB=150°;
⑤S△AOC+S△AOB=6+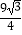 .
.
其中正确的结论是( )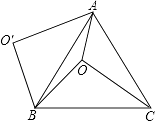
A.②③④⑤
B.①③④⑤
C.①②③⑤
D.①②④⑤
相关试题

