Question

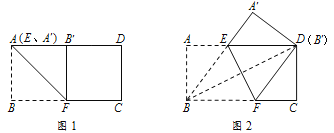
【题目】把一张矩形纸片ABCD按如图方式折叠，使顶点B落在边AD上（记为点B′），点A落在点A′处，折痕分别与边AD、BC交于点E、F．

（1）试在图中连接BE，求证：四边形BFB′E是菱形；

（2）若AB＝8，BC＝16，求线段BF长能取到的整数值．

Answer 1

【答案】（1）证明见解析（2）8，9，10

【解析】试题分析：（1）连接BB′，由折叠知点B、B′关于EF对称，可知BE＝B′E，BF＝B′F，然后根据矩形的性质可证∠B′EF＝B′FE，从而得到BE＝B′E＝B′F＝BF，再由四条边都相等的四边形是菱形得证；

（2）如图1，当点E与点A重合时，四边形ABFB′是正方形，此时BF最小；如图2，当点B与点D重合时，BF最大，然后由勾股定理可求出范围，然后取整即可.

试题解析：（1）连接BB′．由折叠知点B、B′关于EF对称．

∴EF是线段BB′的垂直平分线．

∴BE＝B′E，BF＝B′F．

∵四边形ABCD是矩形，

∴AD∥BC．

∴∠B′EF＝∠BFE．

由折叠得B′FE＝∠BFE．

∴∠B′EF＝B′FE．

∴B′E＝B′F．

∴BE＝B′E＝B′F＝BF．

∴四边形BFB′E是菱形．

（2）如图1，当点E与点A重合时，四边形ABFB′是正方形，此时BF最小．

∵四边形ABFB′是正方形，

∴BF＝AB＝8，即BF最小为8．

如图2，当点B与点D重合时，BF最大．

设BF＝，则CF＝，DF＝BF＝．

在Rt△CDF中，由勾股定理得CF2＋CD2＝DF2．

∴＝，解得＝10，即BF＝10．

∴8≤BF≤10．

∴线段BF长能取到的整数值为8，9，10．