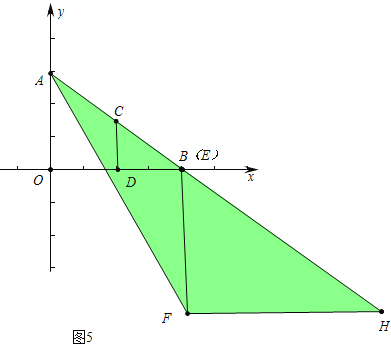
【题目】如图,在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA,点E从点A出发,以每秒1个单位的速度向B运动,到点B停止,AE=EF,运动时间为t(s).
(1)在Rt△EFH中,EF= ,EH= ,点F坐标为( , )(用含t的代数式表示)
(2)t为何值时,H与C重合?
(3)设△EFH与△CDB重叠部分图形的面积为S(S>0),求S与t的函数关系式。
(4)在整个运动过程中,Rt△EFH扫过的面积是多少?

参考答案:
【答案】(1)EF=t,EH=![]() 点F坐标为
点F坐标为![]() ;
;
(2)t=![]() 时,H与C重合;
时,H与C重合;
(3)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
(4)Rt△EFH扫过的面积是![]() .
.
【解析】试题分析:(1)作EM⊥OA垂足为M,由△EFH∽△AOB,得![]() ,可以求出EH,由EM∥OB,得
,可以求出EH,由EM∥OB,得![]() ,可以解决点F坐标.
,可以解决点F坐标.
(2)根据AE+EH=AC,列出方程即可解决.
(3)分三种情形:①如图2中,FH与CD交于点M,当![]() 时,②如图3中,
时,②如图3中, ![]() <t≤5时,S=S△CDB=6,③如图4中,当5<t≤10时,画出图象求出重叠部分面积即可.
<t≤5时,S=S△CDB=6,③如图4中,当5<t≤10时,画出图象求出重叠部分面积即可.
(4)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=![]() FH(AO+BF),由此即可计算.
FH(AO+BF),由此即可计算.
试题解析:(1)如图1中,作EM⊥OA垂足为M,
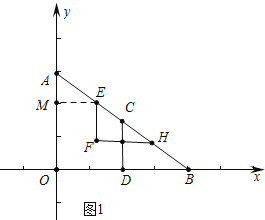
∵AE=EF=t,AO=6,BO=8,∠AOB=90°,
∴AB=![]() =10.
=10.
∵∠AOB=∠EFH=90°,∠EHF=∠ABO,
∴△EFH∽△AOB,
∴![]() ,即
,即![]() ,
,
∴EH=![]() t,
t,
∵EM∥OB,
∴![]() ,
,
∴AM=![]() t,EM=
t,EM=![]() t,
t,
∴点F坐标(![]() t,6-
t,6-![]() t).
t).
(2)如图2中,当点H与点C重合时,
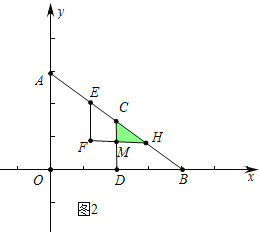
AE+EH=AC,
∴t+![]() t=5,
t=5,
∴t=![]()
∴t=![]() 时,点H与点C重合.
时,点H与点C重合.
(3)当点H与点B重合时,AE+EH=AB,
∴t+![]() t=10,
t=10,
∴t=![]() ,
,
当点E与点C重合时,t=5,
当点E与点B重合时,t=10,
①如图2中,FH与CD交于点M,当![]() ≤t≤
≤t≤![]() 时,
时,
∵CH=EH-EC=EH-(AC-AE)=![]() t-5+t=
t-5+t=![]() t-5.CM=
t-5.CM=![]() CH=
CH=![]() t-3,MH=
t-3,MH=![]() CH=
CH=![]() t-4,
t-4,
∴S=![]() CMMH=
CMMH=![]() (
(![]() t-3)(
t-3)(![]() t-4)=
t-4)=![]() t2-
t2-![]() t+6.
t+6.
②如图3中, ![]() <t≤5时,S=S△CDB=6,
<t≤5时,S=S△CDB=6,
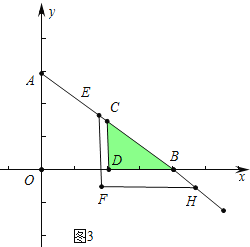
③如图4中,当5<t≤10时,
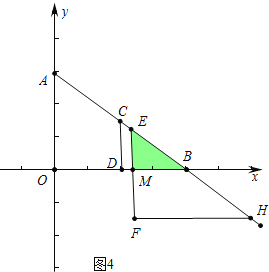
∵EB=AB-AE=10-t,EM=![]() EB=6-
EB=6-![]() t,BM=
t,BM=![]() EB=8-
EB=8-![]() t,
t,
∴S=![]() EMMB=
EMMB=![]() (6-
(6-![]() t)(8-
t)(8-![]() t)=
t)=![]() (10-t)2.
(10-t)2.
综上所述: ![]() ,
, ![]() ,
, ![]()
(4)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=![]() FH(AO+BF)=
FH(AO+BF)=![]() ×
×![]() ×16=
×16=![]() .
.
-
科目: 来源: 题型:
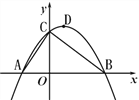
查看答案和解析>>【题目】如图,已知点A的坐标为(-2,0),直线
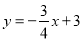 与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线
与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线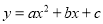 过A、B、C三点.
过A、B、C三点.(1)求抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标.
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2-(x+a)(x+b)-3的值与x的取值无关,则a,b一定满足( )
A. a=0且b=0 B. ab=0
C. ab=1 D. a+b=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 5是25的平方根 B. 125的立方根是±5
C. -0.125的立方根是-0.5 D. (-5)3的立方根是-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2)
(2)﹣6÷(﹣ )×
)× 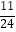
(3)( ﹣
﹣  ﹣
﹣ 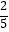 )×105
)×105
(4)﹣14+[1﹣(1﹣0.5× )]×[2﹣(﹣3)2].
)]×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标平面内有下列三条直线:
①经过点(0,2)且平行于x轴的直线;
②直线y=2x﹣8;
③经过点(0,12)且平行于直线y=﹣2x的直线,
其中经过点(5,2)但不经过第三象限的直线共有( )
A.0条
B.1条
C.2条
D.3条 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A,B,C.则下列结论正确的个数有( )
①∠AOB+∠BOC=45°;②BC=2AB;③OB2=10AB2;④OC2=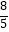 OB2 .
OB2 . 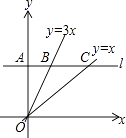
A.1个
B.2个
C.3个
D.4个
相关试题

