【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2 , 点A,B的对应点分别为点D,E.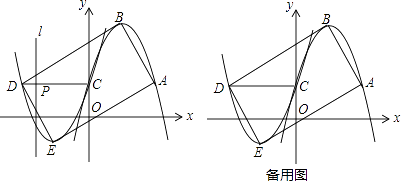
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
参考答案:
【答案】
(1)
解:由题意得:
将A(m,1)代入y1=ax2﹣2ax+1得:am2﹣2am+1=1,
解得:m1=2,m2=0(舍),
∴A(2,1)、C(0,1)、D(﹣2,1);
(2)
解:如图1,
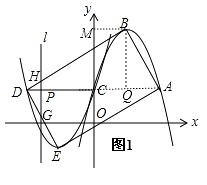
由(1)知:B(1,1﹣a),过点B作BM⊥y轴,
若四边形ABDE为矩形,则BC=CD,
∴BM2+CM2=BC2=CD2,
∴12+(﹣a)2=22,
∴a= ![]()
![]() ,
,
∵y1抛物线开口向下,
∴a=﹣ ![]() ,
,
∵y2由y1绕点C旋转180°得到,则顶点E(﹣1,1﹣ ![]() ),
),
∴设y2=a(x+1)2+1﹣ ![]() ,则a=
,则a= ![]() ,
,
∴y2= ![]() x2+2
x2+2 ![]() x+1;
x+1;
(3)
解:如图2,
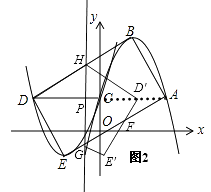
当0≤t≤1时,则DP=t,构建直角△BQD,
得BQ= ![]() ,DQ=3,则BD=2
,DQ=3,则BD=2 ![]() ,
,
∴∠BDQ=30°,
∴PH= ![]() t,PG=
t,PG= ![]() t,
t,
∴S= ![]() (PE+PF)×DP=
(PE+PF)×DP= ![]() t2,
t2,
如图2,当1<t≤2时,EG=E′G= ![]() (t﹣1),E′F=2(t﹣1),
(t﹣1),E′F=2(t﹣1),
S不重合= ![]() (t﹣1)2,
(t﹣1)2,
S=S1+S2﹣S不重合= ![]() +
+ ![]() (t﹣1)﹣
(t﹣1)﹣ ![]() (t﹣1)2,
(t﹣1)2,
=﹣ ![]()
综上所述:S= ![]() t2(0≤t≤1)或S=﹣
t2(0≤t≤1)或S=﹣ ![]() (1<t≤2).
(1<t≤2).
【解析】本题考查了二次函数的性质,旋转的性质和矩形对角线的性质,以及三角函数及特殊角的应用,综合性较强;善于从已知中挖掘隐藏条件是本题的关键:如此题可以计算矩形的边长及对角线与边的夹角,得出30°,以此为突破口,将需要的边长用t表示,得出函数关系式;另外本题还运用了分类讨论的思想,这在二次函数中运用较多,应熟练掌握.(1)直接将点A的坐标代入y1=ax2﹣2ax+1得出m的值,因为由图象可知点A在第一象限,所以m≠0,则m=2,写出A,C的坐标,点D与点A关于点C对称,由此写出点D的坐标;(2)根据顶点坐标公式得出抛物线y1的顶点B的坐标,再由矩形对角线相等且平分得:BC=CD,在直角△BMC中,由勾股定理列方程求出a的值得出抛物线y1的解析式,由旋转的性质得出抛物线y2的解析式;(3)分两种情况讨论:①当0≤t≤1时,S=S△GHD=S△PDH+S△PDG , 作辅助线构建直角三角形,求出PG和PH,利用面积公式计算;②当1<t≤2时,S=S直角三角形+S矩形﹣S不重合 , 这里不重合的图形就是△GE′F,利用30°角和60°角的直角三角形的性质进行计算得出结论.
【考点精析】通过灵活运用二次函数的性质和矩形的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E

(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形AOB是由三角形A1O1B1平移后得到的,已知点A的坐标为(2,-2),点B的坐标为(-4,2),若点A1的坐标为(3,-1).
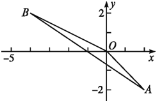
求:(1)O1,B1的坐标.
(2)三角形AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为3,E是BC上一点,BE=
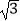 ,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( )
,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( ) 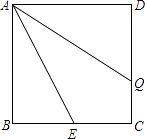
A.3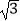 ﹣3
﹣3
B.3﹣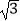
C.
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x=5x﹣5
(2)4x+3(2x﹣3)=12﹣(x﹣4)
(3)
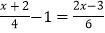 .
.(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
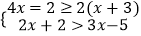 ,并求其整数解.
,并求其整数解.
相关试题

