【题目】已知正方形ABCD的边长为3,E是BC上一点,BE= ![]() ,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( )
,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( ) 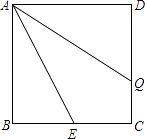
A.3 ![]() ﹣3
﹣3
B.3﹣ ![]()
C.![]()
D.3
参考答案:
【答案】A
【解析】解:如图所示: 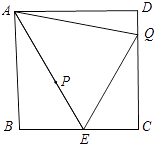
在Rt△ABE中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
∵BC=3,BE= ![]() ,
,
∴EC=3﹣ ![]() .
.
由翻折的性质可知:PE=CE=3﹣ ![]() .
.
∵AP+PE≥AE,
∴AP≥AE﹣PE.
∴当点A、P、E一条直线上时,AP有最小值.
∴AP=AE﹣PE=2 ![]() ﹣(3﹣
﹣(3﹣ ![]() )=3
)=3 ![]() ﹣3.
﹣3.
故选:A.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形AOB是由三角形A1O1B1平移后得到的,已知点A的坐标为(2,-2),点B的坐标为(-4,2),若点A1的坐标为(3,-1).
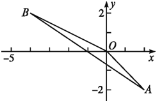
求:(1)O1,B1的坐标.
(2)三角形AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2 , 点A,B的对应点分别为点D,E.
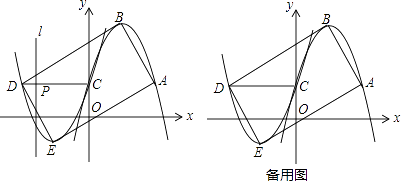
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x=5x﹣5
(2)4x+3(2x﹣3)=12﹣(x﹣4)
(3)
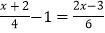 .
.(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
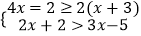 ,并求其整数解.
,并求其整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)请补全频数分布直方图;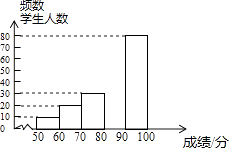
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
相关试题

