【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
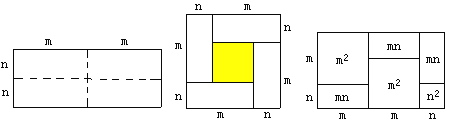
图① 图② 图③
(1)你认为图②中的阴影部分的正方形的边长等于________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;
方法②: ;
(3)请你观察图②,利用图形的面积写出![]() 、
、![]() ,
, ![]() 这三个代数式之间的等量关系: ;
这三个代数式之间的等量关系: ;
(4)根据(3)中的结论,若![]() ,
, ![]() ,则
,则![]() ;
;
(5)有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了![]()
![]() .
.
试画出一个几何图形,使它的面积能表示: ![]()
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;
; ![]() ;(3)
;(3)![]() =
=![]() ;(4)
;(4)![]()
【解析】试题分析:(1)正方形的边长=小长方形的长-宽;
(2)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(m+n)2-4mn=(m-n)2可求解;
(4)利用(x-y)2=(x+y)2-4xy,再求x-y,即可解答.
(5)根据多项式画出图形,即可解答.
解:(1)由图可知边长为:m-n;
(2)(m+n)2-4mn,(m-n)2;
(3)(m+n)2-4mn=(m-n)2;
(4)(x-y)2=(x+y)2-4xy,
∵x+y=-8,xy=3.75,
∴(x-y)2=64-15=49,
∴x-y=±7,
(5)如图,
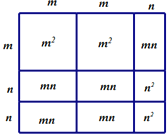
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠C=α,∠EAC+∠FBC=β
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则α与β有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与α、β的关系是______.(用α、β表示)
(3)如图③,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2 ;依此类推,则∠P5=______.(用α、β表示)



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在折纸活动中,小明制作了一张⊿ABC纸片,点D、E分别是边AB、AC上,将⊿ABC沿着DE折叠压平,A与A’重合,若∠A=75°,则∠1+∠2=( )
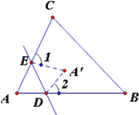
A. 150° B. 210° C. 105° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是: ;
(4)图中,能使S△ABQ=S△ABC的格点Q(点Q不与点C重合),共有 个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题7分)一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“冈”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“黄”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率为P2,请直接写出P2的值,并比较P1,P2的大小.(2+3+2=7)
-
科目: 来源: 题型:
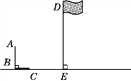
查看答案和解析>>【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
相关试题

