【题目】阅读下面的例题及点拨,补全解题过程(完成点拨部分的填空),并解决问题:例题:如图1,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°
点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连结EM,易证△ABM≌△EBM( ),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠ =∠ ;
由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠ .
又因为∠2+∠6=120,所以∠5+∠6=120°,所以∠AMN=60°.
问题:如图3,四边形ABCD的四条边都相等,四个角都等于90°,M是BC边上一点(不含端点B,C),N是四边形ABCD的外角∠DCH的平分线上一点,且AM=MN.求∠AMN的度数.

参考答案:
【答案】点拨:SAS,3,4,5.问题:∠AMN=90°.
【解析】
点拨:根据全等知识及角度转换补全证明过程即可;问题:延长AB至E,使EB=AB,连接EM、EC,则EB=BC,∠EBM=∠ABM=90°,得出△EBC是等腰直角三角形,由等腰直角三角形的性质得出∠BEC=∠BCE=45°,证出∠BCE+∠MCN=180°,得出E、C、N,三点共线,由SAS证明△ABM≌△EBM得出AM=EM,∠1=∠2,得出EM=MN,由等腰三角形的性质得出∠3=∠4,证出∠1=∠2=∠5,得出∠5+∠6=90°,即可得出结论.
解:点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连结EM,易证△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;
由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5.
又因为∠2+∠6=120°,所以∠5+∠6=120°,所以∠AMN=60°.
问题:延长AB至E,使EB=AB,连接EM、EC,如图所示:
则EB=BC,∠EBM=∠ABM=90°,
∴△EBC是等腰直角三角形,
∴∠BEC=∠BCE=45°,
∵N是正方形ABCD的外角∠DCH的平分线上一点,
∴∠MCN=90°+45°=135°,
∴∠BCE+∠MCN=180°,
∴E、C、N,三点共线,
在△ABM和△EBM中, ,
,
∴△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2,
∵AM=MN,
∴EM=MN,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠AMN=180°﹣90°=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,如杨辉三角就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数降幂排列)的系数规律例如,在三角形中第一行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3ab+3ab2+b3展开式中的系数.结合对杨辉三角的理解完成以下问题
(1)(a+b)2展开式a2+2ab+b2中每一项的次数都是 次;
(a+b)3展开式a3+3a2b+3ab2+b3中每一项的次数都是 次;
那么(a+b)n展开式中每一项的次数都是 次.
(2)写出(a+1)4的展开式 .
(3)拓展应用:计算(x+1)5+(x﹣1)6+(x+1)7的结果中,x5项的系数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中,  ,
,  ,
,  ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作 交BC边于点F,联结EF.
交BC边于点F,联结EF.(1)如图1,当
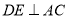 时,求EF的长;
时,求EF的长;(2)如图2,当点E在AC边上移动时,
 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出 的正切值;
的正切值;(3)如图3,联结CD交EF于点Q,当
 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )

A.9
 B.12C.8D.8
B.12C.8D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )

A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
相关试题

