【题目】如图①,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25cm/s的速度沿BC向终点C运动,两点到达终点后停止运动。过点P作PE∥BC交AD于点E,连结EQ,设动点运动的时间为ts(t>0)。
(1) 连结DP,经过1s后,四边形EQDP能够成为平行四边形吗? 请说明理由;
(2) 当t为何值时,△EDQ为直角三角形?
(3) 如图②,设点M是EQ的中点,在点P、Q的整个运动过程中,试探究点M的运动路径长度是多少?

参考答案:
【答案】(1)能.四边形EQDP是平行四边形. (2)当t为2.5或3.1时,△EDQ为直角三角形(3)点M的运动路径长度是![]() cm
cm
【解析】试题分析:(1)如图1,当t=1时,AP=1,BQ=1.25,QD=0.75.由PE∥DC,得到EP=0.75,从而有EP=QD,再由EP∥QD,即可得到结论;
(2)分∠EQP=90°,∠QED=90°两种情况,通过三角形相似,列出比例关系,求出t的值即可;
(3)作AB的中点M,DC的中点M′,连接MM′,则M运动的路径就是线段MM′.过M作MG⊥BC于G.可以证明MG是△ABC的中位线,得到MG=2,BG=GC=2.5.再由M′是DC的中点,得到M′C=1.5,进而得到GM′=2.5-1.5=1,在Rt△MGM′中,由勾股定理即可得出MM′的长.
试题解析:解:(1)能.理由如下:
如图1,当t=1时,AP=1,BQ=1.25,QD=2-1.25=0.75.∵PE∥DC,∴ ![]() ,∴
,∴![]() ,∴EP=0.75,∴EP=QD.∵EP∥QD,∴四边形EQDP是平行四边形.
,∴EP=0.75,∴EP=QD.∵EP∥QD,∴四边形EQDP是平行四边形.

(2)分两种情况讨论:
①如图3,当∠EQD=90°时,显然有EQ=PC=4﹣t.又∵EQ∥AC,∴△EDQ∽△ADC,
∴![]() .∵BC=5厘米,CD=3厘米,∴BD=2厘米,∴DQ=1.25t﹣2,∴
.∵BC=5厘米,CD=3厘米,∴BD=2厘米,∴DQ=1.25t﹣2,∴![]() ,解得t=2.5(秒);
,解得t=2.5(秒);
②如图4,当∠QED=90°时,作EM⊥BC于M,CN⊥AD于N,则四边形EMCP是矩形,EM=PC=4﹣t.在Rt△ACD中,∵AC=4厘米,CD=3厘米,∴AD=![]() =5,∴CN=
=5,∴CN=![]() =
=![]() .∵∠CDA=∠EDQ,∠QED=∠C=90°,∴△EDQ∽△CDA,∴
.∵∠CDA=∠EDQ,∠QED=∠C=90°,∴△EDQ∽△CDA,∴![]() ,∴
,∴![]() ,解得t=3.1(秒).
,解得t=3.1(秒).
综上所述:当t=2.5秒或t=3.1秒时,△EDQ为直角三角形.

(3)作AB的中点M,DC的中点M′,连接MM′,则M运动的路径就是线段MM′.过M作MG⊥BC于G.∵M是AB的中点,∴G是BC的中点,∴MG是△ABC的中位线,∴MG=![]() AC=2,BG=GC=2.5.∵M′是DC的中点,∴M′C=
AC=2,BG=GC=2.5.∵M′是DC的中点,∴M′C=![]() DC=1.5,∴GM′=2.5-1.5=1,∴MM′=
DC=1.5,∴GM′=2.5-1.5=1,∴MM′=![]() =
=![]() =
=![]() (cm).
(cm).

-
科目: 来源: 题型:
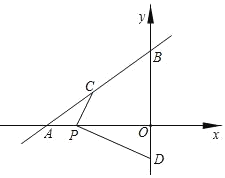
查看答案和解析>>【题目】如图,直线
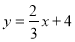 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①AB//CD;②AB=CD;③BC//AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有哪几种,请一一写出_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我校七年级某班准备买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副
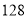 元,乒乓球每盒
元,乒乓球每盒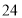 元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的
元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的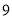 折优惠这个班级需要球拍
折优惠这个班级需要球拍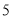 副,乒乓球
副,乒乓球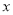 盒(
盒(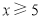 ).
).(1)分别求甲、乙两家商店购买这些商品所箭的费用(用含x的代数式表示);
(2)当
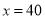 时,购买所需商品去哪家商店合算?请通过计算说明理由.
时,购买所需商品去哪家商店合算?请通过计算说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板如图放置 其中∠ACB=∠DEC=90,∠A=45,∠D=30,斜边 AB=4,CD=5,把三角板DCE绕点C顺时针旋转15得到三角形D1CE (如图二),此时AB与CD1交于点O,则线段AD1的长度为( )

A.
 B.
B.  C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出以下结论:①abc<0;②b2-4ac>0;③4b+c<0;④若B(-
 ,y1),C(-
,y1),C(- ,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)
,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)
相关试题

