【题目】如图,已知![]() ,
,![]() ,
,![]() 、
、![]() 相交于
相交于![]() .
.
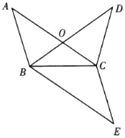
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() 的度数________;
的度数________;
(3)作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
参考答案:
【答案】(1)见详解;(2)64°;(3)见详解
【解析】
(1)由AAS,即可判断三角形全等;
(2)根据等腰三角形的性质和全等三角形的性质得∠OCB=∠OBC=32°,再根据三角形外角的性质,即可求解;
(3)易证△ABC≌△DCB,得AC=BD,再根据轴对称图形的性质,得DC=CE,BD=BE,进而根据平行四边形的判定定理,即可得到结论.
(1)在△AOB与△DOC中,
∵ ,
,
∴△AOB≌△DOC(AAS);
(2)∵AB=BC,∠A=32°,
∴∠ACB=∠A=32°,
∵△AOB≌△DOC,
∴OB=OC,
∴∠OCB=∠OBC=32°,
∴∠AOB=∠OCB+∠OBC=64°,
故答案是:64°;
(3)∵△AOB≌△DOC,
∴OB=OC,
∴∠OCB=∠OBC,
∵∠A=∠D,AB=DC,
∴△ABC≌△DCB(AAS),
∴AC=BD,
∵△BDC,△BEC关于直线BC对称,
∴DC=CE=AB,BD=BE=AC,
∴四边形ABEC是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述正确的是( )
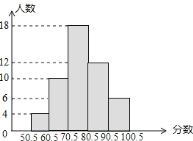
A.抽样的学生共60人
B.60.5~70.5这一分数段的频数为12
C.估计这次测试的及格率(60分为及格)在92%左右
D.估计优秀率(80分以上为优秀)在32%左右
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:tan60°+|
 ﹣2|+(
﹣2|+(  )﹣1﹣(π+2)0 .
)﹣1﹣(π+2)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:

(1)本次调查中,一共调查了_____名同学;
(2)条形统计图中,m=_____,n=_______;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是______度;
(4)学校计划购买课外读物5000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)
 +
+ =0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=2S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在直线BD上移动时(不与B,D重合)直接写出∠BAP,∠DOP,∠APO之间满足 的数量关系.
-
科目: 来源: 题型:
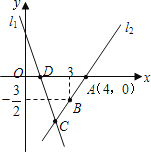
查看答案和解析>>【题目】如图,直线
 的表达式为:
的表达式为: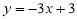 ,且
,且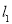 与
与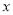 轴交于点
轴交于点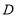 ,与
,与 轴交于点
轴交于点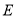 ,直线
,直线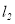 的表达式为
的表达式为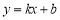 ,
,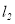 经过点
经过点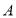 ,
,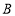 ,
,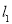 ,
,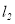 交于点
交于点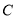 .
.
(1)求直线
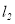 的函数表达式;
的函数表达式;(2)直接写出点
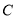 的坐标________;
的坐标________;(3)如果点
 在直线
在直线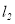 上,满足
上,满足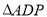 的面积是
的面积是 面积的2倍,求点
面积的2倍,求点 的坐标;
的坐标;(4)把
 向左平移
向左平移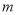 个单位到
个单位到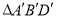 的位置,当
的位置,当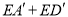 取得最小值时,直接写出
取得最小值时,直接写出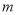 的值
的值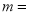 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货27吨,2辆大货车与6辆小货车一次可以运货28吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨;
(2)目前有45吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运货费用150元,每辆小货车一次运货费用100元,请问货运公司应如何安排车辆最节省费用?
相关试题

