【题目】已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA),B(0,yB),C(﹣1,yC)在该抛物线上,当y0≥0恒成立时,![]() 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 4 D. 3
参考答案:
【答案】D
【解析】
主要是要是通过相似三角形边的对应关系,构造所求的式子,并对结果找到限制条件即可
 由0<2a<b,得x0=﹣
由0<2a<b,得x0=﹣![]() <﹣1,
<﹣1,
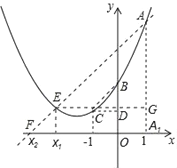
由题意,如图,过点A作AA1⊥x轴于点A1,
则AA1=yA,OA1=1,
连接BC,过点C作CD⊥y轴于点D,则BD=yB﹣yC,CD=1,
过点A作AF∥BC,交抛物线于点E(x1,yE),交x轴于点F(x2,0),
则∠FAA1=∠CBD,
于是Rt△AFA1∽Rt△BCD,
所以![]() =
=![]() ,即
,即![]() =
=![]() ,
,
过点E作EG⊥AA1于点G,
易得△AEG∽△BCD.
有![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∵点A(1,yA)、B(0,yB)、C(﹣1,yC)、E(x1,yE)在抛物线y=ax2+bx+c上,
得yA=a+b+c,yB=c,yC=a﹣b+c,yE=ax12+bx1+c,
∴![]() =
=![]() =1﹣x1,
=1﹣x1,
化简,得x12+x1﹣2=0,解得x1=﹣2(x1=1舍去),
∵y0≥0恒成立,根据题意,有x2≤x1<﹣1,
则1﹣x2≥1﹣x1,即1﹣x2≥3,
∴![]() ≥3,
≥3,
∴![]() 的最小值为3.
的最小值为3.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,使ΔABC≌ΔADC成立的条件是( )

A.AB=AD,∠B=∠DB.AB=AD,∠ACB=ACD
C.BC=DC,∠BAC=∠DACD.AB=AD,∠BAC=∠DAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=6
 ,动点P从点A出发,以每秒
,动点P从点A出发,以每秒 个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.
个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.
(1)当t=1秒时,求动点P、Q之间的距离;
(2)若动点P、Q之间的距离为4个单位长度,求t的值;
(3)若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度为 .
-
科目: 来源: 题型:
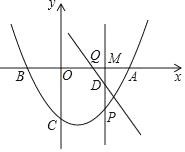
查看答案和解析>>【题目】二次函数y=
 +bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A(4,0)和y轴上点C(0,﹣3).
+bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A(4,0)和y轴上点C(0,﹣3).(1)直接写出b,c,k的值,b= ,c= ,k= ;
(2)二次函数与x轴的另一个交点为B,点M(m,0)在线段AB上运动,过点M作x轴的垂线交直线AC于点D;交抛物线于点P.
①是否存在实数m,使△PCD为直角三角形.若存在、求出m的值;若不存在,请说明理由;
②当0<m<4时,过D作直线AC的垂线交x轴于点Q,求PD+DQ的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )
A. (4,﹣3) B. (﹣4,3) C. (﹣3,4) D. (﹣3,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )

A.

B.

C.
D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一枚棋子放在七角棋盘的第0号角,现依逆时针方向移动这枚棋子,其各步依次移动1,2,3,…,n个角,如第一步从0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角,….若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是( )

A.0 B.1 C.2 D.3
相关试题

