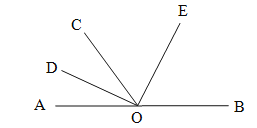
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角?分别是哪些角?
(2)求∠DOB的度数;
(3)请你通过计算说明OE是否平分∠COB?
参考答案:
【答案】(1)图中小于平角的角有9个.它们分别是:∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB;(2)∠DOB=155°;(3)见解析.
【解析】试题分析:(1)根据角的定义即可解决;
(2)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(3)根据∠COE=∠DOE-∠DOC和∠BOE=∠BOD-∠DOE分别求得∠COE与∠BOE的度数即可说明.
试题解析:解:(1)图中小于平角的角有9个.它们分别是:∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB.

(2)∵∠AOC=50°,OD平分∠AOC,∴∠DOC=![]() ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,∴∠BOD=∠DOC+∠BOC=155°.
∠AOC=25°,∠BOC=180°﹣∠AOC=130°,∴∠BOD=∠DOC+∠BOC=155°.
(3)∵∠DOE=90°,∠DOC=25°,∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又∵∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,∴∠COE=∠BOE,即OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
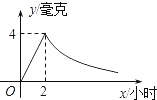
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线y1=klx+b与反比例函数y2=
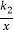 的图象交于A(1,5)、B(5,n)两点,与x轴交于C点,
的图象交于A(1,5)、B(5,n)两点,与x轴交于C点, 
(1)求反比例函数的解析式;
(2)求C点坐标;
(3)请直接写出当y1<y2时,x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形至少有( )
A. 一个锐角 B. 两个锐角 C. 一个钝角 D. 一个直角
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.
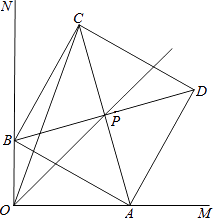
(1)求证:无论点A、点B怎样运动,点P都在∠AOB的平分线上;
(2)若OP=4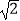 ,求OA的长.
,求OA的长.
(3)求OC的最大值(提示:取AB的中点Q,连接CQ、OQ,运用两点之间,线段最短) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
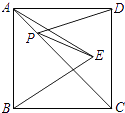
A.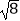
B.3
C.4
D.2
相关试题

