搜索
【题目】学生在素质教育基地进行社会实践活动，帮助农民伯伯采摘了黄瓜和茄子共40kg，了解到这些蔬菜的种植成本共42元，还了解到如下信息： 
（1）请问采摘的黄瓜和茄子各多少千克？
（2）这些采摘的黄瓜和茄子可赚多少元？
参考答案：
【答案】
（1）解：设采摘黄瓜x千克，茄子y千克．根据题意，得
，
解得 
．
答：采摘的黄瓜和茄子各30千克、10千克
（2）解：30×（1.5﹣1）+10×（2﹣1.2）=23（元）．
答：这些采摘的黄瓜和茄子可赚23元
【解析】（1）设他当天采摘黄瓜x千克，茄子y千克，根据采摘了黄瓜和茄子共40kg，了解到这些蔬菜的种植成本共42元，列出方程，求出x的值，即可求出答案；（2）根据黄瓜和茄子的斤数，再求出每斤黄瓜和茄子赚的钱数，即可求出总的赚的钱数．本题考查了二元一次方程组的应用．解题关键是弄清题意，合适的等量关系，列出方程组．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答
（1）先化简再求值：a（1﹣4a）+（2a+1）（2a﹣1），其中a=4．
（2）解不等式组：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】课间，小明拿着老师的等腰三角板玩，不小心掉到两墙之间，如图．
（1）求证：△ADC≌△CEB；
（2）从三角板的刻度可知AC=25cm，请你帮小明求出砌墙砖块的厚度a的大小（每块砖的厚度相等）．
-
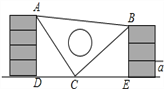
科目： 来源： 题型：
查看答案和解析>>【题目】据图解答
（1）如图1，在菱形ABCD中，CE=CF，求证：AE=AF．
（2）如图2，AB是⊙O的直径，PA与⊙O相切于点A，OP与⊙O相交于点C，连接CB，∠OPA=40°，求∠ABC的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，
，设c为最长边．当
时，△ABC是直角三角形；当
时，利用代数式
和
的大小关系，可以判断△ABC的形状（按角分类）．（1）请你通过画图探究并判断：当△ABC三边长分别为6，8，9时，△ABC为____三角形；当△ABC三边长分别为6，8，11时，△ABC为______三角形．
（2）小明同学根据上述探究，有下面的猜想：“当
时，△ABC为锐角三角形；当
时，△ABC为钝角三角形．” 请你根据小明的猜想完成下面的问题：当
，
时，最长边c在什么范围内取值时，△ABC是直角三角形、锐角三角形、钝角三角形？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，A市到B市的路程为260千米，甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计），乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市，同时甲车以原来1.5倍的速度前往B市，如图是两车距A市的路程y（千米）与甲车所用时间x（小时）之间的函数图象，下列四种说法：
①甲车提速后的速度是60千米/时；
②乙车的速度是96千米/时；
③乙车返回时y与x的函数关系式为y=﹣96x+384；
④甲车到达B市乙车已返回A市2小时10分钟．
其中正确的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着教育信息化的发展，学生的学习方式日益增多，教师为了指导学生有效利用网络进行学习，对学生进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题：
（1）本次接受问卷调查的学生共有人，在扇形统计图中“D“选项所占的百分比为；
（2）扇形统计图中，“B”选项所对应扇形圆心角为度；
（3）请补全条形统计图；
（4）若该校共有1200名学生，请您估计该校学生课外利用网络学习的时间在“A”选项的有多少人？
相关试题
