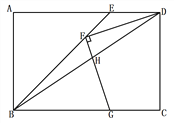
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG, ![]() ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.
参考答案:
【答案】![]()
【解析】过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,过点A作AP⊥BD于点P,延长DF交AB于点K,过点K作KQ⊥BD于点Q,如图所示。

∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM,NF=MG.
∵∠BAD=90°,BE平分∠ABC,
∴∠ABE=∠CBE=45°,
又∵FM⊥BM,
∴FM=BM,
∵BF=![]() ,
,
∴BM=FM=3,MG=BGBM=43=1,
∴NF=MG=1,AB=NM=4,AD=AN+ND=BM+FM=6,
∴BD=![]() .
.
由面积公式可知:S△ABD=![]() BDAP=
BDAP=![]() ABAD,即
ABAD,即![]() AP=4×6,
AP=4×6,
∴AP=![]() ,
,
∵NF∥AB,
∴△DNF∽△DAK,
∴![]() ,
,
∴AK=2NF=2,DK= ![]() =2
=2![]() ,DF=
,DF=![]() =
=![]() .
.
∴BK=ABAK=42=2,
∵KQ∥AP,
∴△BKQ∽△BAP,
∴![]() ,即,
,即,  ,
,
∴KQ=![]() ,
,
∴BQ=![]() =
= =
=![]() ,
,
∴DQ=BDBQ=![]()
![]() =
=![]() ,
,
∵∠DFH=∠DQK=90°,∠FDH=∠QDK,
∴△DFH∽△DQK,
∴![]() ,
,
即 ,
,
∴FH=![]() ,
,
∴GH=FGFH=![]()
![]() =
=![]() .
.
故答案为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.同角的补角相等B.两条直线被第三条直线所截,同位角相等
C.两个无理数的和仍是无理数D.有公共顶点且相等的两个角是对顶角
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.有一个内角是锐角的三角形是锐角三角形B.钝角三角形的三个内角都是钝角
C.有一个内角是直角的三角形是直角三角形D.三条边都相等的三角形称为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每个外角都等于45°,则它的内角和等于( )
A.720°
B.1040°
C.1080°
D.540° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_______处.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将y=2x﹣3的图象向上平移2个单位长度得到的直线表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为__________千米/时

相关试题

