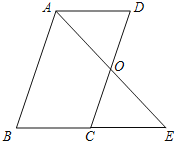
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
参考答案:
【答案】 45 45
【解析】分析:
(1)由已知条件易得∠D=∠OCE,DO=CO,∠AOD=∠COE,由此即可证得△AOD≌△EOC;
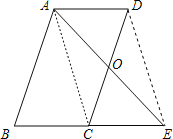
(2)如下图,由△AOD≌△EOC可得AO=EO,DO=BO,从而可得四边形ACED是平行四边形,结合四边形ABCD是平行四边形可得AD=BC=CE,此时要使四边形ACED是正方形,则需∠ACE=90°,AE=CE,故只需∠B=∠AEB=45°即可得到∠BAE=90°,结合BC=CE即可得到所需结论,从而得到四边形ACED是正方形.
详解:
(1)∵点O是CD的中点,
∴DO=CO,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在![]() 和
和![]() 中
中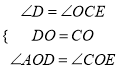 ,
,
∴![]() ≌
≌![]() ;
;
![]() 当
当![]() 和
和![]() 时,四边形ACED是正方形,
时,四边形ACED是正方形,
∵![]() 和
和![]() ,
,
∴![]() ,
,
∵![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形ACED是平行四边形,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴平行四边形ACED是菱形,
∵![]() ,
,
∴![]() ,
,
∴四边形ACED是正方形.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小亮同学设计的一个轴对称图形的一部分,其中点
 都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
都在直角坐标系网格的格点上,每个小正方形的边长都等于1.(1)请画出关于
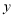 轴成轴对称图形的另一半,并写出
轴成轴对称图形的另一半,并写出 两点的对应点坐标.
两点的对应点坐标.(2)记
 两点的对应点分别为
两点的对应点分别为 ,请直接写出封闭图形
,请直接写出封闭图形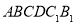 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数
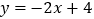 ,下列结论错误的是( )
,下列结论错误的是( )A.函数的图象与
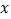 轴的交点坐标是
轴的交点坐标是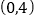
B.函数值随自变量的增大而减小
C.函数的图象不经过第三象限
D.函数的图象向下平移
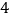 个单位长度得到
个单位长度得到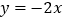 的图象
的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点,且∠DBC=∠BAC,
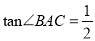 .
.(1) 求证:BD是⊙O的切线;
(2) 求
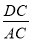 的值;
的值;(3) 如图2,过点B作BG⊥AC交AC于点F,交⊙O于点G,BC、AG的延长线交于点E,⊙O的半径为6,求BE的长.
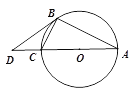
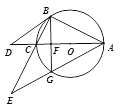
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
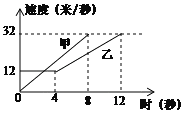
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
相关试题

