搜索
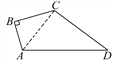
【题目】如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
参考答案：
【答案】36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：解：连接AC．如图所示：
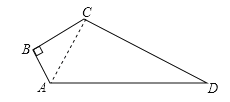
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根据勾股定理得：AC=
=5．又∵CD=12，AD=13，∴AD2=132=169，CD2+AC2=122+52=144+25=169，∴CD2+AC2=AD2，∴△ACD为直角三角形，∠ACD=90°，则S四边形ABCD=S△ABC+S△ACD=
ABBC+ACCD=×3×4+×5×12=36．
故四边形ABCD的面积是36．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元．
（1）求每张门票的原定票价；
（2）根据实际情况，活动组织单位决定对于个人购票也采取优惠政策，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下是某手机店1～4月份的统计图，分析统计图，对3、4月份三星手机的销售情况四个同学得出的以下四个结论，其中正确的为( )
A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较，只能比较该店销售总额
-
科目： 来源： 题型：
查看答案和解析>>【题目】冬季即将来临，是流感的高发期，某中学积极进行班级环境消毒，总务处购买甲、乙两种消毒液共100瓶，购买这两种消毒液共用780元，其中甲种消毒液共用240元，且乙种消毒液的单价是甲种消毒液单价的1.5倍．
（1）求甲、乙两种消毒液的单价各为多少元？
（2）该校准备再次购买这两种消毒液（不包括已购买的100瓶），共140瓶，且所需费用不超过1210元，问甲种消毒液至少要购买多少瓶？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
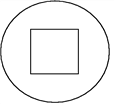
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用勾股定理可以在数轴上画出表示
的点，请依据以下思路完成画图，并保留画图痕迹：第一步：（计算）尝试满足
，使其中a，b都为正整数.你取的正整数a=____，b=________；第二步：（画长为
的线段）以第一步中你所取的正整数a，b为两条直角边长画Rt△OEF，使O为原点，点E落在数轴的正半轴上， 
，则斜边OF的长即为
.请在下面的数轴上画图：（第二步不要求尺规作图，不要求写画法）
第三步：（画表示
的点）在下面的数轴上画出表示
的点M，并描述第三步的画图步骤：_______________________________________________________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O（0，0），B（0，1）是正方形OBB1C的两个顶点，以它的对角线OB1为一边作正方形OB1B2C1 ，以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 ，再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 ，…，依次进行下去，则点B6的坐标是（ ）
A. （﹣8，0） B. （0，﹣8） C. （
，0） D. （
，0）
相关试题
