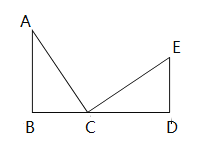
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
参考答案:
【答案】(1)详见解析;(2)60°;(3)△ACE是等腰直角三角形,理由详见解析.
【解析】
(1)根据全等三角形的性质即可求解;
(2)根据全等三角形的性质得到∠ACB=∠CED,再根据直角三角形的性质得到∠BAC+∠ACB=90°,根据已知条件∠CED=2∠BAC,可求出∠BAC=30°,即可得到∠CED=60°.
(3)根据全等三角形的性质即可得到AC⊥CE,AC=CE,故可求解.
(1)∵ △ABC≌△CDE,
∴ AB=CD,BC=DE.
∴ AB+ED=BC+CD=BD. 即BD=AB+ED.
(2)∵ △ABC≌△CDE,
∴ ∠ACB=∠CED.
在△ABC中,∠B=90°,
∴ ∠BAC+∠ACB=90°.
∵ ∠CED=2∠BAC,
∴ 3∠BAC=90°,
∴ ∠BAC=30°,
∴ ∠CED=60°.
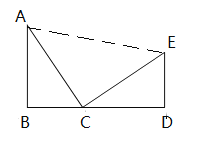
(3)△ACE是等腰直角三角形.
∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD=∠BAC+∠B,即∠ACE+∠DCE=∠BAC+∠B.
∵ ∠BAC=∠DCE,∠B=90°,
∴ ∠ACE=90°.
∵ △ABC≌△CDE,
∴ AC=CE,
∴ △ACE是等腰直角三角形.
-
科目: 来源: 题型:
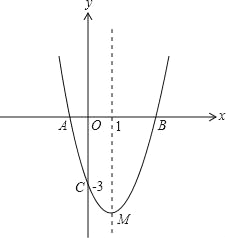
查看答案和解析>>【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价
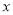 (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于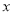 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围); (2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价
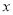 的取值范围;
的取值范围; -
科目: 来源: 题型:
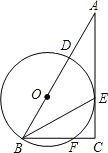
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
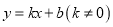 与双曲线
与双曲线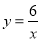 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.(1)求直线
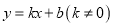 的解析式;
的解析式;(2)若点P在x轴上,且
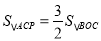 ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).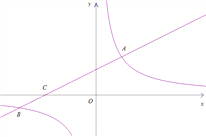
-
科目: 来源: 题型:
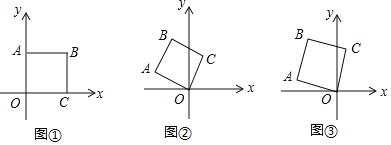
查看答案和解析>>【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用若干等长的木棒按如图的方式摆放.
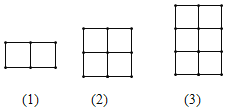
 填写下表:
填写下表:图形编号




木棒根数
7
12
______
______
______

 搭第n个图形需要多少根木棒?
搭第n个图形需要多少根木棒? 搭第几个图形需要2017根木棒?
搭第几个图形需要2017根木棒?
相关试题

