【题目】已知直线l1:y=﹣![]() 与直线l2:y=kx﹣
与直线l2:y=kx﹣![]() 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
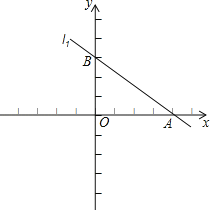
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
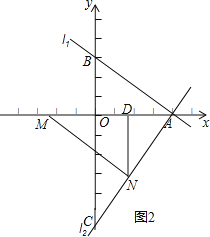
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)k=![]() ,见解析;(2)点P的坐标(
,见解析;(2)点P的坐标(![]() ,
,![]() );(3)当N的纵坐标为(
);(3)当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.
【解析】
试题分析:(1)对于直线l1,令y=0求出x的值,确定出A坐标,代入直线l2求出k的值,作出直线l2图象即可;
(2)设P(a,b),△ACP面积=△ABC面积﹣△BPC面积,根据已知三角形ACP面积求出a的值,进而求出b的值,确定出P坐标即可;
(3)如图2,作ND⊥x轴于D,利用勾股定理求出AC的长,由△ANM≌△AOC,得到对应边相等,表示出AM,AN,MN,确定出△AMN为直角三角形,利用面积法求出ND的长,确定出N纵坐标,进而求出横坐标,确定出N坐标即可.
解:(1)∵直线l1:y=﹣![]() x+3与x轴交于点A,
x+3与x轴交于点A,
∴令y=0时,x=4,即A(4,0),
将A(4,0)代入直线l2:y=kx﹣![]() ,得k=
,得k=![]() ,
,
直线l2图象如图1所示;
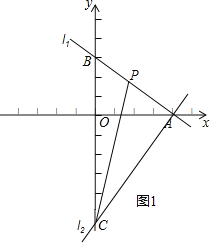
(2)设P(a,b),
根据题意得:S△ACP=S△ABC﹣S△PBC=![]() ×(3+
×(3+![]() )×4﹣
)×4﹣![]() ×(3+
×(3+![]() )a=15,
)a=15,
解得:a=![]() ,
,
将P(![]() ,b)代入直线l1得:b=
,b)代入直线l1得:b=![]() ×(﹣
×(﹣![]() )+3=﹣
)+3=﹣![]() +3=
+3=![]() ,
,
∴点P的坐标(![]() ,
,![]() );
);
(3)如图2,作ND⊥x轴于D,
∵AC=![]() =
=![]() ,△ANM≌△AOC,
,△ANM≌△AOC,
∴AM=AC=![]() ,AN=AO=4,MN=OC=
,AN=AO=4,MN=OC=![]() ,∠ANM=∠AOC=90°,
,∠ANM=∠AOC=90°,
∵S△AMN=![]() AMND=
AMND=![]() ANMN,
ANMN,
∴ND=![]() =
=![]() =
=![]() ,
,
将N的纵坐标y=﹣![]() 代入直线l2得:x=
代入直线l2得:x=![]() ,
,
∴当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x分别取﹣
 、﹣
、﹣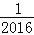 、﹣
、﹣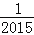 、…、﹣
、…、﹣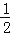 、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式
、﹣2、﹣1、0、1、2、…、2015、2016、2017时,计算分式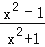 的值,再将所得结果相加,其和等于 .
的值,再将所得结果相加,其和等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果获利100元记作+100元,那么支出200元记作
A、+200元 B、-200元 C、+100元 D、-100元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知C、D是线段AB上的两个点,M、N分别为AC、BD的中点.
(1)若AB=10cm,CD=4cm,求AC+BD的长及M、N的距离.
(2)如果AB=a,CD=b,用含a、b的式子表示MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是 岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每个外角都为36°,则这个多边形的内角和是_______°
-
科目: 来源: 题型:
查看答案和解析>>【题目】君畅中学计划购买一些文具送给学生,为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中,你最需要的文具是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据以上信息回答下列问题:
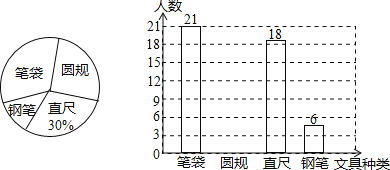
(1)在这次调查中,最需要圆规的学生有多少名?并补全条形统计图;
(2)如果全校有970名学生,请你估计全校学生中最需要钢笔的学生有多少名?
相关试题

