搜索
【题目】当x分别取﹣
、﹣
、﹣
、…、﹣
、﹣2、﹣1、0、1、2、…、2015、2016、2017时，计算分式
的值，再将所得结果相加，其和等于 ．
参考答案：
【答案】﹣
．
【解析】
试题分析：
=
=﹣
=﹣（1﹣
）=
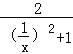﹣1把x是分数的情况代入，
=
=1﹣
把x是整数时代入，然后求值即可．
解：=
=﹣
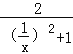=﹣（1﹣
）=
﹣1，
=
=1﹣
，
则当x=﹣
、﹣
、﹣
、…、﹣
时，代入后所得结果的和是【
﹣1】+【
﹣1】+…+【
﹣1】=
+
+…+
﹣2016，
x=﹣2、﹣1、0、1时，代入所得的式子的和是：【1﹣】+【1﹣
】+【1﹣
】+【1﹣】=
+0﹣1﹣0=﹣
．
当x=2、…、2015、2016、2017时，代入所得结果的和是【1﹣
】+…+【1﹣
】+【1﹣
】=+0+0﹣0﹣（+
+…+
+
）+2016=2016﹣（++…+
）
则x分别取﹣
、﹣
、﹣
、…、﹣
、﹣2、﹣1、0、1、2、…、2015、2016、2017时，计算分式
的值，再将所得结果相加是﹣．
故答案是：﹣．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某农户承包荒山若干亩种果树2000棵，每年需对果园投资7800元，水果年总产量为18000千克，此水果在市场上每千克售a元，在果园自助销售每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克，需3人帮忙，每人每天付工资80元，农用车运费及其他各项税费平均每天60元，假定两种方式都能将水果全部销售出去．
（1）直接写出一年中两种方式出售水果的总销售金额是多少元．（用含a，b的最简式子表示）
（2）若a=1.3元，b=1.1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好？
（3）为了提高收益，该农户明年准备增加投入资金加强果园管理，预计每增加投入1元，水果产量增加5千克，力争到明年纯收入达到16500元，而且该农户采用了（2）中较好的出售方式出售，销售单价与（2）一样，那么该农户要增加投资多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：数轴上A、B两点表示的有理数分别为a、b，且（a﹣1）2+|b+2|=0，
（1）求（a+b）2015的值．
（2）数轴上的点C与A、B两点的距离的和为7，求点C在数轴上表示的数c的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一组数据5，4，2，5，6的中位数是（ ）
A．5 B．4 C．2 D．6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果获利100元记作＋100元，那么支出200元记作
A、＋200元 B、－200元 C、＋100元 D、－100元
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知C、D是线段AB上的两个点，M、N分别为AC、BD的中点．
（1）若AB=10cm，CD=4cm，求AC+BD的长及M、N的距离．
（2）如果AB=a，CD=b，用含a、b的式子表示MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l1：y=﹣
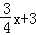与直线l2：y=kx﹣
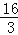交于x轴上的同一个点A，直线l1与y轴交于点B，直线l2与y轴的交点为C．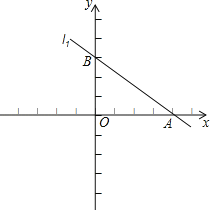
（1）求k的值，并作出直线l2图象；
（2）若点P是线段AB上的点且△ACP的面积为15，求点P的坐标；
（3）若点M、N分别是x轴上、线段AC上的动点（点M不与点O重合），是否存在点M、N，使得△ANM≌△AOC？若存在，请求出N点的坐标；若不存在，请说明理由．
相关试题
