Question

【题目】已知正方形ABCD和正方形CEFG，连结AF交BC于点O，点P是AF的中点，过点P作PH⊥DG于H，CD=2，CG=1．

（1）如图1，点D、C、G在同一直线上，点E在BC边上，求PH的长；

（2）把正方形CEFG绕着点C逆时针旋转α（0°＜α＜180°）

①如图2，当点E落在AF上时，求CO的长；

②如图3，当DG=时，求PH的长．

Answer 1

【答案】（1）PH=；（2）①CO= ；②PH=．

【解析】试题分析：（1）先判断出四边形APGF是梯形，再判断出PH是梯形的中位线，得到PH=（FG+AD）；

（2）①先判断出△COE∽△AOB，得到AO是CO的2倍，设出CO，表示出BO，AO，再用勾股定理计算，②先找出辅助线，再判断出△ARD≌△DSC，△CSG≌△GTF，求出AR+FT，最后用梯形中位线即可．

试题解析：（1）PH⊥CD，AD⊥CD，

∴PH∥AD∥FG，

∵点P是AF的中点，

∴PH是梯形APGF的中位线，

∴PH=（FG+AD）=，

（2）①∵∠CEO=∠B=90°，∠COE=∠AOB，

∴△COE∽△AOB，

∴，

∴，

设CO=x，

∴AO=2x，BO=2﹣x，

在△ABO中，根据勾股定理得，4+（2﹣x）2=（2x）2，

∴x=或x=（舍），

∴CO=x=．

②如图3，

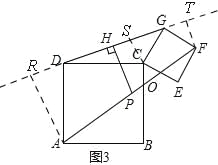
分别过点A，C，F作直线DG的垂线，垂足分别为R，S，T，

∵∠ADR+∠CDS=90°，∠CDS+∠DCS=90°，

∴∠ADR=∠DCS，

∵∠ADR=∠CSD=90°，

∵AD=CD

∴△ARD≌△DSC，

∴AR=DS，

同理：△CSG≌△GTF，

∴SG=FT，

∴AR+FT=DS+SG=DG=，

同（1）的方法得，PH是梯形ARTF的中位线，

∴PH=（AR+FT）=．