【题目】已知抛物线y=ax2+2x﹣3经过点(1,3)
(1)求a的值;
(2)当x=3时,求y的值;
(3)求这个抛物线的对称轴和顶点坐标.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+2x﹣3经过点(1,3),
∴a×12+2×1﹣3=3,
∴a=4
(2)解:由(1)得抛物线y=4x2+2x﹣3,
当x=3时,得y=4×32+2×3﹣3=39
(3)解:∵y=4x2+2x﹣3=4(x+ ![]() )2﹣
)2﹣ ![]() ,
,
∴抛物线对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)把点的坐标代入可得到关于a的值,可求得a;(2)把x=3代入函数解析式可求得y的值;(3)把抛物线解析式化为顶点式可求得其对称轴和顶点坐标.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣
 ,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号)
,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程.
(1)x2﹣6x+5=0;
(2)2x2+3x﹣5=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,D在CB上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE=( )
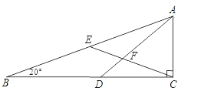
A. 40° B. 50° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.

(1)求证:△ADE≌△CDF;
(2)填空:△CDF可以由△ADE绕旋转中心点,按逆时针方向旋转度得到;
(3)若BC=3,AE=1,求△DEF的面积.
相关试题

