【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG,请判断BE与DG的关系,并证明。

参考答案:
【答案】垂直且相等
【解析】试题分析:
延长GD交BE于点M,由已知条件易证△BCE≌△DCG,可得BE=DG,∠BEC=∠DGC;再由∠CDG+∠DGC=90°,∠CDG=∠EDM可得∠BEC+∠EDM=90°,从而可得∠EMD=90°,可到GD⊥BE.
试题解析:
BE与DG的关系是:垂直且相等,理由如下:
∵四边形ABCD与四边形ECGF都是正方形,
∴EC=CG,∠BCE=∠DCG=90°,BC=CD,
∴△BCE≌△DCG(SAS),
∴BE=DG,∠BEC=∠DGC,
又∵∠CDG+∠DGC=90°,∠CDG=∠EDM,
∴∠BEC+∠EDM=90°,
∴∠EMD=180°-90°=90°,
∴GD⊥BE,即BE与DG的关系是垂直且相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
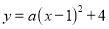 与
与 轴交于点A、B,与
轴交于点A、B,与 轴交于点C.过点C作CD//
轴交于点C.过点C作CD//  轴交抛物线的对称轴于点D,抛物线对称轴交x轴于点E,连接BD.已知点A的坐标为
轴交抛物线的对称轴于点D,抛物线对称轴交x轴于点E,连接BD.已知点A的坐标为 .
.(1)求抛物线的解析式;(2)求四边形COBD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)若点Q在x轴正半轴上,且∠ADQ=∠DAC,求出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑销售商试销某一品牌电脑(出厂价为3000元∕台)以4000元∕台销售时,平均每月可销售100台,现为了扩大销售,销售商决定降价销售在原一月份销售量的基础上,经二月份的市场调查,三月份降价销售(保证不亏本)后,月销售额达到576000元,已知电脑价格每台下降100元,月销售量将上升10台。
(1)求一月份到三月份销售额的月平均增长率?
(2)求三月份时,该电脑的销售价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的余角是54°38′,则这个角的补角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若□ABCD的对角线AC、BD的长是关于x的一元二次方程
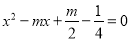 的两个实数根.
的两个实数根.(1)当m为何值时,□ABCD是矩形?求出此时矩形的对角线长?
(2)当□ABCD的一条对角线AC=2时,求另外一条对角线的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】气象台预报“本市明天降水概率是85%”,对此信息,下列说法正确的是( )
A.本市明天将有85%的地区降水 B.本市明天将有85%的时间降水
C.明天降水的可能性比较大 D.明天肯定下雨
相关试题

