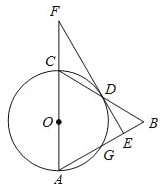
【题目】如图,在△ABC中,以AC边为直径作⊙O交BC边于点D,交AB于点G,且D是BC中点,DE⊥AB,交AB于点E,交AC的延长线交于点F.
(1)求证:直线EF是⊙O的切线.
(2)若CF=3,cos∠CAB=![]() ,求⊙O的半径和线段BD的长.
,求⊙O的半径和线段BD的长.
参考答案:
【答案】(1)证明见解析;(2)⊙O的半径为![]() ,BD的长为
,BD的长为![]() .
.
【解析】
(1)根据三角形的中位线定理证明OD∥AB,可得OD⊥EF,所以直线EF是⊙O的切线;
(2)设⊙O的半径为r,根据cos∠FOD=cos∠CAB=![]() ,求得r的值,根据平行线分线段成比例定理得:
,求得r的值,根据平行线分线段成比例定理得:![]() ,可得AE的长,并计算BE的长,证明△BDE∽△BAD,则
,可得AE的长,并计算BE的长,证明△BDE∽△BAD,则![]() ,代入可得BD的长.
,代入可得BD的长.
(1)证明:连接OD.
∵OA=OC,DB=DC,∴OD∥AB.
∵DE⊥AB,∴OD⊥EF,∴直线EF是⊙O的切线.
(2)如图,连接AD,设⊙O的半径为r.
在Rt△ODF中,∵cos∠FOD=cos∠CAB=![]() =
=![]() =
=![]() =
=![]() ,∴r=
,∴r=![]() ,∴AB=2DO=9.
,∴AB=2DO=9.
∵OD∥AB,∴![]() ,即
,即![]() =
=![]() ,AE=
,AE=![]() ,∴BE=AB﹣AE=9﹣
,∴BE=AB﹣AE=9﹣![]() =
=![]() .
.
∵AC为⊙O的直径,∴∠ADE+∠BDE=∠ADB=90°.
∵DE⊥AB,∴∠B+∠BDE=90°,∴∠ADE=∠B,∴△BDE∽△BAD,∴![]() ,∴BD2=AB
,∴BD2=AB![]() =
=![]() ,∴BD=
,∴BD=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ,BD的长为
,BD的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB=a,且BD=BE.
(1)求证:AC=AD+CE;
(2)若a=120°,点F在直线l的上方,△BEF为等边三角形,补全图形,请判断△ACF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料,两次购买饲料价格分别为m元/千克和n元/千克,且m≠n,两名采购员的采购方式也不同,其中甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?(用字母m、n表示)
(2)谁的购货方式更合算?
-
科目: 来源: 题型:
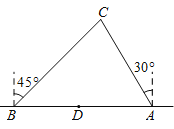
查看答案和解析>>【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(
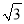 +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”.
例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.

(1)如图1,在△ABC中,D是边BC上一点,若∠B=30°,∠BAD=∠C=40°,求证: AD为△ABC的“等角分割线”;
(2)如图2,△ABC中,∠C=90°,∠B=30°;
①画出△ABC的“等角分割线”,写出画法并说明理由;
②若BC=3,求出①中画出的“等角分割线”的长度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割线”CD,直接写出所有符合要求的∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
相关试题

