【题目】已知数轴上两个点A、B所对应的数为a、b,且a、b满足![]() .
.
(1)求AB的长;

(2)若甲、乙分别从A、B两点同时在数轴上相向运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,求甲乙相遇点所表示的数;

(3)若点C对应的数为—1,在数轴上A点的左侧是否存在一点P,使PA+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由。

参考答案:
【答案】(1)7 (2)-1 (3)-4
【解析】
(1)利用绝对值的性质以及偶次方的性质得出即可;(2)利用当两点同时向左移动时或当两点同时相向移动时,分别求出即可;(3)利用P点的位置得出PA,BP,PC的长进而得出等式求出即可.
(1)![]() ,
,
∴a+3=0,b-4=0,
解得:a=-3,b=4,
∴AB=4-(-3)=7.
(2)设x秒时两点相遇,则
5x+2x=7,
解得:x=1,
∴此时对应点为:-3-(-2)=-1,
故甲乙相遇点所表示的数为:-1;
(3)存在.
∵点C对应的数为-1,在数轴上A点的左侧一点P,使PA+PB=3PC,
∴设P点对应数为x,则4-x+(-3-x)=3(-1-x),
解得:x=-4,
∴点P所对应的数为-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)—2+(—3)—(+5)+(+7);
(2)(—4)×7×(—1);
(3)
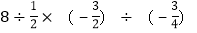 ;
; (4)
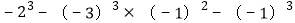 .
.(5)
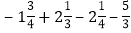 ;
; (6)
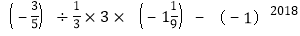
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=
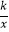 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.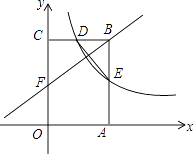
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3,P是AC上一动点,则PB+PE的最小值是( ).

A. 5 B. 5
 C. 6 D.
C. 6 D. 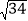
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.

(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的括号里:
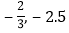 ,5,
,5, ,
, ,0,8,-2,-0.7
,0,8,-2,-0.7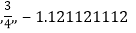 ……
……正数集合{________________________________________…};
负数集合{________________________________________…};
有理数集合{________________________________________…};
无理数集合{________________________________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=a+(-b)=∣a-b∣;

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 .
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=2,那么x为 ;
(3)当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是 .
相关试题

