【题目】综合题:探索发现
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD .
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC= ![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD= ![]() .
.
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样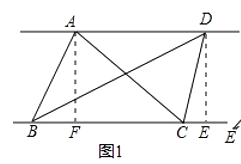
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD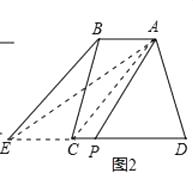
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2 , 则图中阴影三角形的面积是cm2 . 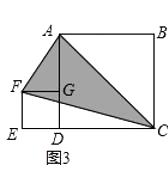
参考答案:
【答案】
(1)同底等高的两三角形面积相等
(2)证明:∵AB∥CE,BE∥AC,
∴四边形ABEC为平行四边形,
∴△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED
(3)40
【解析】解;(1)利用图形直接得出:同底等高的两三角形面积相等;
所以答案是:同底等高的两三角形面积相等;(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,
∵S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF= ![]() ×b×(a﹣b)+b×b+
×b×(a﹣b)+b×b+ ![]() ×a×a﹣
×a×a﹣ ![]() ×b×(b+a)=
×b×(b+a)= ![]() ab﹣
ab﹣ ![]() b2+b2+
b2+b2+ ![]() a2﹣
a2﹣ ![]() b2﹣
b2﹣ ![]() ab=
ab= ![]() a2,
a2,
∴S△ACF= ![]() S正方形ABCD=
S正方形ABCD= ![]() ×80cm2=40cm2;
×80cm2=40cm2;
所以答案是:40.
【考点精析】掌握三角形的面积和平行四边形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车0.8小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园,如图是他们离家的路程
 与离家时间
与离家时间 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题: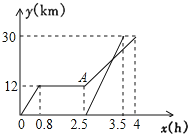
(1)小明家到和平公园的路程为
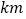 ,他在书城逗留的时间为
,他在书城逗留的时间为  ;
;(2)图中
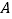 点表示的意义是 ;
点表示的意义是 ;(3)求小明的妈妈驾车的平均速度(平均速度=
 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
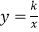 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当x=2时,求y的值;
(3)当自变量x从5增大到8时,函数值y是怎样变化的? -
科目: 来源: 题型:
查看答案和解析>>【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段
 ,点
,点 为线段
为线段 的中点,点
的中点,点 为线段
为线段 上任意一点(
上任意一点( 不与
不与 重合),分别以
重合),分别以 和
和 为边在
为边在 的下方作正方形
的下方作正方形 和正方形
和正方形 ,以
,以 和
和 为边在线段下方作正方形
为边在线段下方作正方形 和正方形
和正方形 ,则正方形
,则正方形 与正方形
与正方形 的面积之和等于正方形
的面积之和等于正方形 和正方形
和正方形 面积之和的两倍.
面积之和的两倍.(1)请你画出正方形
 和正方形
和正方形 (不必尺规作图);
(不必尺规作图);(2)设
 ,
, ,根据题意写出关于
,根据题意写出关于 的等式并证明.
的等式并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12016 +
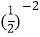 3.14 π 0
3.14 π 0 (2) 3a2 3 2a a5
(3) x 2 x 1 3xx 1
(4)2a b c2a b c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、B、C在坐标轴上,且A、B、C的坐标分别为
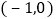 、
、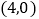 、
、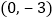 过点A的直线AD与y轴正半轴交于点D,
过点A的直线AD与y轴正半轴交于点D,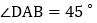
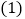 求直线AD和BC的解析式;
求直线AD和BC的解析式;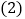 如图2,点E在直线
如图2,点E在直线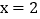 上且在直线BC上方,当
上且在直线BC上方,当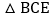 的面积为6时,求E点坐标;
的面积为6时,求E点坐标;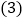 在
在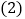 的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当
的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当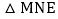 周长最小时,求
周长最小时,求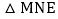 周长的最小值.
周长的最小值.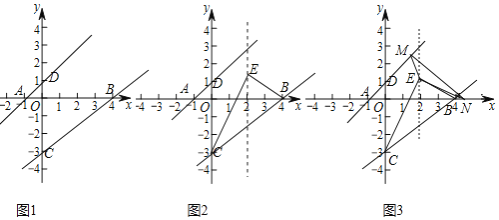
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
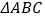 中,BC的垂直平分线EF交
中,BC的垂直平分线EF交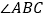 的平分线BD于点E,若
的平分线BD于点E,若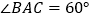 ,
, ,那么
,那么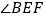 的大小是( )
的大小是( )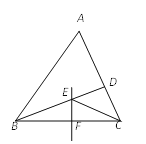
A.
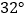 B.
B. 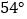 C.
C. 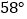 D.
D. 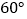
相关试题

